HDU-5963 朋友 思维

题目链接http://acm.hdu.edu.cn/showproblem.php?pid=5963

吐槽

这道题我第一眼看，嗯？？博弈论？还是树上的？我好像不会啊。。。但是一想某人的话，感觉这个应该也不会太难，可能有规律

分析

于是我就从样例开始仔细思考找规律，第一个样例应该是看不出来啥，但第二个内容量就比较丰富了。但我模拟完样例二依旧没发现什么，难道这道题真要建个线段树什么的？？接着我把关注点放到了输出上，输出只有两种，那是不是应该存在某种奇偶关系？还是要先考虑链的情况，因为从无根树上的一个点出发遍历就相当于走几条链（好像树的问题大部分都跟链有关）。下面模拟一下



首先要注意到题目中的暗示，每次都要找一个到父亲节点权值为1的点，这就说明了这个问题的限制，它总会结束。先不考虑修改，如果以1为根，不难看出女孩会赢，其中一种走法是







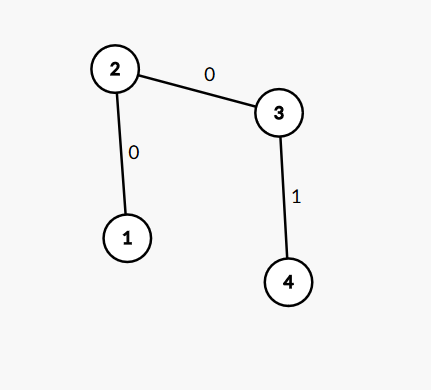
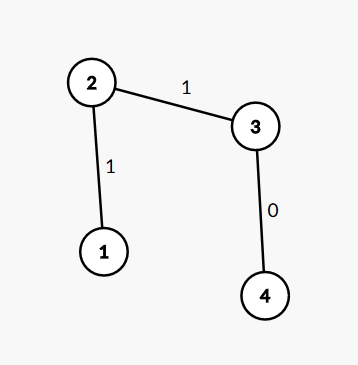
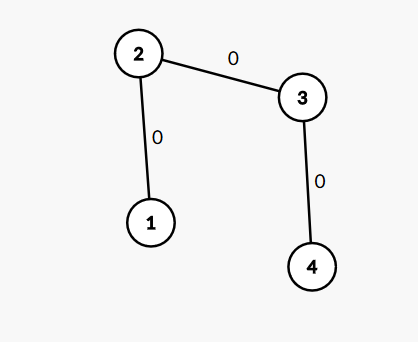
当然也有别的走法，但总会是女生赢。

如果以2为根呢？不难得出还是女孩赢，其中一种走法为







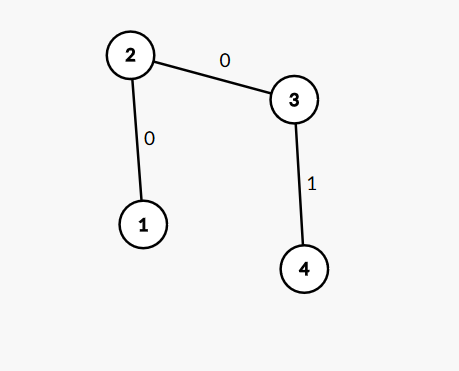
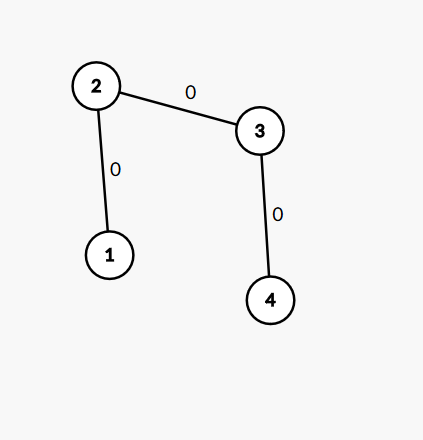
那么是不是图中边权为1的边数为偶数时，就是女生赢呢？仍旧以2为根，我们在4后边再跟一个节点。



会发现这样还是女生赢。

那在根节点2后边跟这个节点呢？



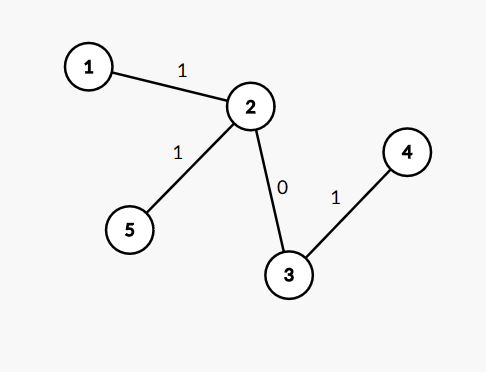
这时候再去模拟就会发现是男生赢了。所以我们猜测，让女生赢的并不是图中边权为1的边数，而是根节点周围边权为1的边数，根据这个大胆的猜测，我写出了下面的代码，好像还白写了一个加边函数。如果你去用样例测试，发现是对的，所以我兴奋的交了上去，WA

#include<cstdio>
#include<cstring>
using namespace std;
const int N=4e4+10;
struct Edge{
    int to,nxt,val;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b,int c){
    e[++len].to=b;e[len].val=c;
    e[len].nxt=Head[a];Head[a]=len;
}
int cnt[N];
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n,m;
        scanf("%d%d",&n,&m);
        memset(cnt,0,sizeof(cnt));
        for(int i=1;i<n;i++){
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            cnt[a]+=c;
            cnt[b]+=c;
        }
        for(int i=1;i<=m;i++){
            int op,x,y,z;
            scanf("%d",&op);
            if(op==1){
                scanf("%d%d%d",&x,&y,&z);
                if(z==1)cnt[x]++,cnt[y]++;
                else cnt[x]--,cnt[y]--;
            }
            else {
                scanf("%d",&x);
                if(cnt&1)printf("Girls win!\n");
                else printf("Boys win!\n");
            }
        }
    }
}

二次分析

既然这个代码过了样例，就说明它应该不是偶然，所以应该是我少考虑了什么。再回去读了一边题，发现题中并没有说当\(op==1\)时，变换的权值与原来的权值相等，也就是说如果我每次都把1变为0，0变为1，那么我上边的代码是可以的，也就是样例情况，但问题就出在它可能是1变为1，0变为0，所以每次必须扫描一边根周围的边权之和，即下边的代码。

#include<cstdio>
#include<cstring>
using namespace std;
const int N=4e4+10;
struct Edge{
    int to,nxt,val;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b,int c){
    e[++len].to=b;e[len].val=c;
    e[len].nxt=Head[a];Head[a]=len;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n,m;
        scanf("%d%d",&n,&m);
        memset(Head,0,sizeof(Head));
        len=0;
        for(int i=1;i<n;i++){
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            Ins(a,b,c);Ins(b,a,c);
        }
        for(int i=1;i<=m;i++){
            int op,x,y,z;
            scanf("%d",&op);
            if(op==1){
                scanf("%d%d%d",&x,&y,&z);
                for(int i=Head[x];i;i=e[i].nxt)
                    if(e[i].to==y)e[i].val=z;
                for(int i=Head[y];i;i=e[i].nxt)
                    if(e[i].to==x)e[i].val=z;
            }
            else {
                int cnt=0;
                scanf("%d",&x);
                for(int i=Head[x];i;i=e[i].nxt)cnt+=e[i].val;
                if(cnt&1)printf("Girls win!\n");
                else printf("Boys win!\n");
            }
        }
    }
}

证明

写完之后感觉就这么过去的话不是很好，万一猜错了就很尴尬，所以想一下证明。

为了简化问题，我们只把链的情况证明了就好。如果连接根节点的边权值为1，其余边有两种情况，一是全为1的，二是含0的，分开讨论一下。

如果含有0，



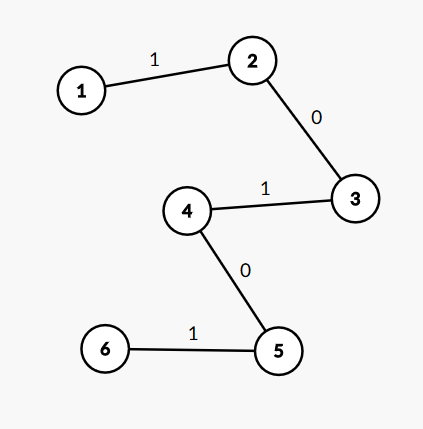
因为是女生先任意选点，所以让女生选择最后一个点，这样连接根节点的那条边就会被置为0，而因为含有0，所以肯定还会剩下边权为1的，这时由于男生不得不去变换边，所以一定会去变换权值为1的，由于根节点在男生变换的时候为0，所以这样的话只有可能是女生让根节点变为0，也就是只有女生会赢。

如果不含0都是1呢？那女生就可以一次性让男生没的变换，仍然是女生赢。

当连接根节点的边权值为0时就会反过来，证毕。