POJ 2826 An Easy Problem?! --计算几何，叉积

题意： 在墙上钉两块木板，问能装多少水。即两条线段所夹的中间开口向上的面积（到短板的水平线截止）

解法： 如图：

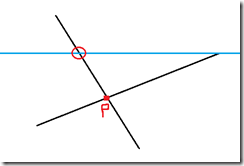
先看是否相交，不相交肯定不行，然后就要求出P与A,B / C,D中谁形成的向量是指向上方的。

然后求出y值比较小的，建一条水平线，求出与另一条的交点，然后求面积。

要注意的是：

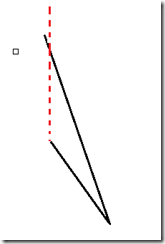
这种情况是不能装水的，要判掉。

还有 交G++会WA， 交C++就可以了， 不知道是POJ的问题还是 G++/C++的问题。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define eps 1e-8
using namespace std;

struct Point{
    double x,y;
    Point(double x=, double y=):x(x),y(y) {}
    void input() { scanf("%lf%lf",&x,&y); }
};
typedef Point Vector;
int dcmp(double x) {
    if(x < -eps) return -;
    if(x > eps) return ;
    return ;
}
template <class T> T sqr(T x) { return x * x;}
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }
bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }
bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) ==  && dcmp(a.y-b.y) == ; }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }

bool SegmentIntersection(Point A,Point B,Point C,Point D) {
    return max(A.x,B.x) >= min(C.x,D.x) &&
           max(C.x,D.x) >= min(A.x,B.x) &&
           max(A.y,B.y) >= min(C.y,D.y) &&
           max(C.y,D.y) >= min(A.y,B.y) &&
           dcmp(Cross(C-A,B-A)*Cross(D-A,B-A)) <=  &&
           dcmp(Cross(A-C,D-C)*Cross(B-C,D-C)) <= ;
}
void SegIntersectionPoint(Point& P,Point a,Point b,Point c,Point d) //需保证ab,cd相交
{
    P.x = (Cross(d-a,b-a)*c.x - Cross(c-a,b-a)*d.x)/(Cross(d-a,b-a)-Cross(c-a,b-a));
    P.y = (Cross(d-a,b-a)*c.y - Cross(c-a,b-a)*d.y)/(Cross(d-a,b-a)-Cross(c-a,b-a));
}
//Data Segment
Point A,B,C,D;
//Data Ends

int main()
{
    int t,i,j;
    scanf("%d",&t);
    while(t--)
    {
        A.input(), B.input(), C.input(), D.input();
        if(!SegmentIntersection(A,B,C,D)) { puts("0.00"); continue; }
        Point P,Insec;
        SegIntersectionPoint(P,A,B,C,D);
        Vector PA = A-P, PB = B-P;
        Vector PC = C-P, PD = D-P;
        Point S1,S2,S3,S4,K1,K2;

        if(dcmp(PA.y) > )      K1 = A;
        else if(dcmp(PB.y) > ) K1 = B;
        else { puts("0.00"); continue; }

        if(dcmp(PC.y) > )      K2 = C;
        else if(dcmp(PD.y) > ) K2 = D;
        else { puts("0.00"); continue; }

        S3 = Point(K1.x,K1.y), S4 = Point(K1.x,);
        if(SegmentIntersection(S3,S4,P,K2)) { puts("0.00"); continue; }
        S3 = Point(K2.x,K2.y), S4 = Point(K2.x,);
        if(SegmentIntersection(S3,S4,P,K1)) { puts("0.00"); continue; }

        if(dcmp(K1.y-K2.y) < )
        {
            S1 = Point(-,K1.y), S2 = Point(,K1.y);
            SegIntersectionPoint(Insec,S1,S2,P,K2);
            printf("%.2f\n",fabs(Cross(K1-P,Insec-P)*0.5));
        }
        else
        {
            S1 = Point(-,K2.y), S2 = Point(,K2.y);
            SegIntersectionPoint(Insec,S1,S2,P,K1);
            printf("%.2f\n",fabs(Cross(K2-P,Insec-P)*0.5));
        }
    }
    return ;
}