Codeforces 1045F Shady Lady 凸包+数学

题目链接：https://codeforc.es/contest/1045/problem/F

题意：先给出一个系数不确定的二元多项式，Borna可以给这个多项式的每一项填上正的系数，Ani能从这个多项式中删除一项。询问删除一项后该多项式是否存在下界（即最小值趋向于\(-\infty\)还是等于一个不为无穷小的数值）。

题解：首先我们可以发现偶数项（x项和y项次数均为偶）都存在下界，只有奇数项（x项和y项）可以不存在下界，问题就是如何判断奇数项能否导出\(-\infty\)。

然后经过一通分（乱）析（搞），我们发现如果把x项的系数\(a_i\)和y项的系数\(b_i\)看做点\((a_i,b_i)\)，那当且仅当所有点和原点构成的凸包上存在奇数点时该多项式能趋向于\(-\infty\)。接下来我们证明这个结论。

• 当凸包上全是偶数点时，多项式存在下界
  
  如下图，凸包上全是偶点，凸包内存在奇数点时，凸包内的奇数点向量坐标可以用凸包上的点表示。如图中\(G\)点，\(H\)点。简单的数学想法：我们设凸包上除原点外共有\(k\)个点，每个点坐标为\(P1(a_1,b_1)\) , \(P2(a_i,b_i)\) , ... , \(P_k(a_k,b_k)\)。则凸包内任意一点\(Q(a,b)\)坐标可表示为\(Q = \sum_{i=1}^kc_iP_i\)（\(c_i\)为大于等于0的常数）。如果这个点在凸包外，那么存在系数\(c_j\)小于零。

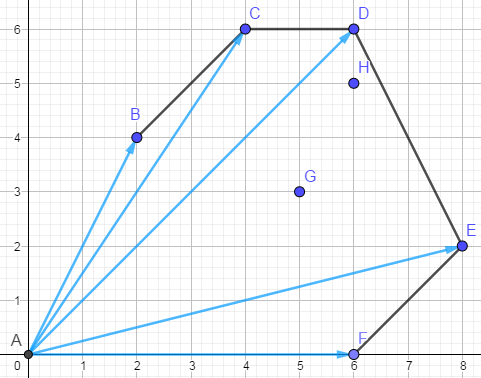
由此，我们可以得到：

\(\sum_{i=1}^kx^{kc_ia_i}y^{kc_ib_i}\ge\vert x^{\sum_{i=1}^kc_ia_i}y^{\sum_{i=1}^kc_ib_i}\vert\) \(\Leftrightarrow\) \(\vert x^{a}y^{b}\vert\) （均值不等式）

也就是说，凸包上的点必定能抵消凸包内的点。

• 当凸包上存在奇数点时，多项式可以不存在下界
  
  我们先假设\((x,y)\)的取值为\((-t^p,t^q)\)，则某一奇数项\(x^{a}y^{b}\)转变为\(-t^{(ap+bq)}\)，而\((ap+bq) = (a,b)\cdot(p,q)\)，因此我们只需要找到\((a,b)\)点乘\((p,q)\)向量最大的情况。
  
  如下图，若存在奇数点（图中为D点）则必定有一条直线能够仅通过该点而不穿越凸包。我们作一条垂线，取向量\(\vec{AH}\)为\((p,q)\)。并且此时\((p,q)\)向量点乘任何凸包上的点均小于\(\vec{AH}\cdot\vec{AD}\)，即该奇数点是高阶无穷小。

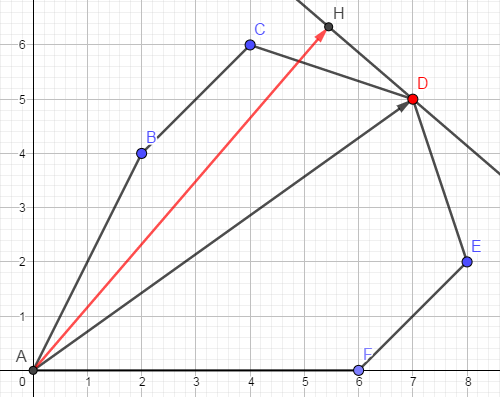
证毕。由此，本题转化为在凸包上删除一点后生成的新凸包上是否存在奇数点。暴力枚举每个点显然会T，但是可以发现删除凸包上一点只会影响该点引出的两条线，也就是说该点边上的两个点仍然在凸包上，因此我们可以用黑白染色的方法来优化。即先直接跑一次凸包；然后删除第1, 3, 5, 7, ... 号点跑一次凸包；再删除第2, 4, 6, 8, ... 号点跑一次凸包。这样就不会影响每个被删除点边上的两个点。总共跑3次凸包，即可得出结果。

AC代码：

#include <bits/stdc++.h>
#define SIZE 300007
#define rep(i, a, b) for(int i = a; i <= b; ++i)
using namespace std;
typedef long long ll;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
ll n, m, t, num; int k;
map<pair<ll, ll>, int> mp;
struct Point {
	ll x, y;
	int num;
	bool flag = false;
};
Point p[SIZE], ch[SIZE], tp[SIZE];
bool cmp(Point a, Point b) {	//andrew算法排序预处理函数
	if (a.x == b.x) return a.y < b.y;
	else return a.x < b.x;
}
ll cross(Point a, Point b, Point c) { return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); }
int andrew(Point p[], Point ch[], ll n) {	//安德鲁算法求凸包，返回顶点数
	sort(p + 1, p + n + 1, cmp);
	ll top = 0;
	for (int i = 1; i <= n; ++i) {
		while ((top > 1) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
		ch[++top] = p[i];
	}
	ll tmp = top;
	for (int i = n - 1; i; --i) {
		while ((top > tmp) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
		ch[++top] = p[i];
	}
	if (n > 1) top--;
	return top;
}
void draw(int top, Point ch[], Point p[]) { //染色操作
	rep(i, 2, top) {
		p[mp[make_pair(ch[i].x, ch[i].y)]].num = 1; ++i;
		p[mp[make_pair(ch[i].x, ch[i].y)]].num = 2;
	}
	p[1].num = 0;
}
void preset(int s){ //把染色后的点丢进tp数组中
    k = 1;
	rep(i, 1, n) {
		if (p[i].num == s) continue;
		tp[k++] = p[i];
	}
}
bool judge(int top, Point ch[]) {   //判断凸包上是否存在奇数点
	rep(i, 1, top)
		if (!ch[i].flag)
			return true;
	return false;
}

int main() {
	io();
	cin >> n; ++n;
	p[1].flag = true; mp[make_pair(0, 0)] = 1;
	rep(i, 2, n) {
		cin >> p[i].x >> p[i].y;
		if ((p[i].x == 0) && (p[i].y == 0)) { --i, --n; continue; } //避免(0,0)点重复出现
		if (((p[i].x % 2) == 0) && ((p[i].y % 2) == 0)) p[i].flag = true;  //标记偶数点
	}
	int top = andrew(p, ch, n);
	rep(i, 1, n) mp[make_pair(p[i].x, p[i].y)] = i; //用map标记路径
	draw(top, ch, p);
	if (judge(top, ch)) { puts("Ani"); return 0; }
	preset(1);
	top = andrew(tp, ch, k - 1);
	if (judge(top, ch)) { puts("Ani"); return 0; }
	preset(2);
	top = andrew(tp, ch, k - 1);
	if (judge(top, ch)) { puts("Ani"); return 0; }
	puts("Borna");
}