luoguP4709 信息传递 置换 + 多项式exp

---

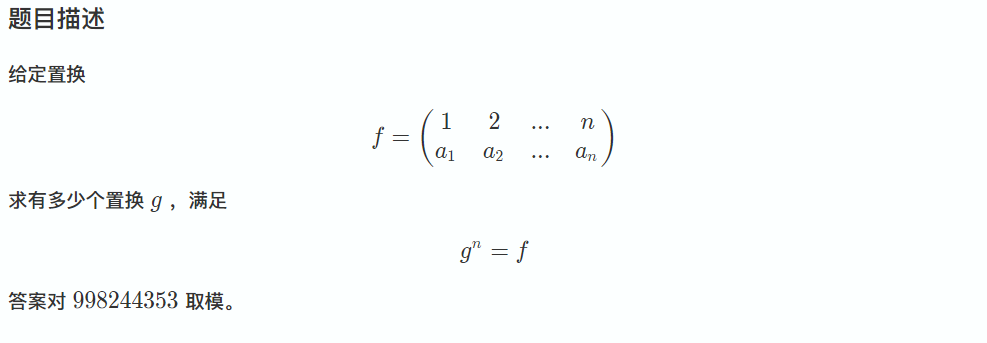
感觉我的做法并不是最优做法...

考虑一个置换\(g\)中的一个置换环\(S\)

在\(g^n\)的形态中，它变为了\(gcd(n, |S|)\)个长度相同的置换环

那么，我们考虑对\(f\)的所有置换环考虑

所有的长度相同的置换环都可以合并

如果\(a\)个长度为\(b\)的置换环合并成一个环，那么方案数为\(b^{a - 1} (a - 1)!\)

需要判掉不合法的情况

其意义是考虑第一个置换以及固定第一个元素，其他任意选择

以这个弄出指数生成函数\(F(x)\)，那么对于长度为\(b\)的合并方案就是\(e^{F(x)} [num(b)]\)\

对于每个长度都这么讨论即可

复杂度\(O(n \log n)\)

---

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

#define ll long long
#define ri register int
#define rec(io, ed) for(ri io = 0; io < ed; io ++)
#define rep(io, st, ed) for(ri io = st; io <= ed; io ++)
#define drep(io, ed, st) for(ri io = ed; io >= st; io --)

#define gc getchar
inline int read() {
    int p = 0, w = 1; char c = gc();
    while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); }
    while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc();
    return p * w;
}

const int sid = 3e5 + 5;
const int mod = 998244353;

inline void inc(int &a, int b) { a += b; if(a >= mod) a -= mod; }
inline void dec(int &a, int b) { a -= b; if(a < 0) a += mod; }
inline int mul(int a, int b) { return 1ll * a * b % mod; }
inline int fp(int a, int k) {
    int ret = 1;
    for( ; k; k >>= 1, a = mul(a, a))
        if(k & 1) ret = mul(ret, a);
    return ret;
}

int n, rev[sid];
int vis[sid], nc[sid], p[sid];

inline void init(int Mn, int &N, int &lg) {
    N = 1, lg = 0;
    while(N < Mn) N <<= 1, lg ++;
}

inline void NTT(int *a, int n, int opt) {
    rec(i, n) if(i < rev[i]) swap(a[i], a[rev[i]]);
    for(ri i = 1; i < n; i <<= 1)
    for(ri j = 0, g = fp(3, (mod - 1) / (i << 1)); j < n; j += (i << 1))
    for(ri k = j, G = 1; k < i + j; k ++, G = mul(G, g)) {
        int x = a[k], y = mul(G, a[i + k]);
        a[k] = (x + y >= mod) ? x + y - mod : x + y;
        a[i + k] = (x - y <0) ? x - y + mod : x - y;
    }
    if(opt == -1) {
        reverse(a + 1, a + n);
        int ivn = fp(n, mod - 2);
        rec(i, n) a[i] = mul(a[i], ivn);
    }
}

int iva[sid], ivb[sid];
inline void Inv(int *a, int *b, int n) {
    if(n == 1) { b[0] = fp(a[0], mod - 2); return; }
    Inv(a, b, n >> 1);
    int N = 1, lg = 0; init(n + n, N, lg);
    rec(i, N) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (lg - 1));
    rec(i, N) iva[i] = ivb[i] = 0;
    rec(i, n) iva[i] = a[i], ivb[i] = b[i];
    NTT(iva, N, 1); NTT(ivb, N, 1);
    rec(i, N) iva[i] = ((ivb[i] << 1) % mod - mul(iva[i], mul(ivb[i], ivb[i])) + mod) % mod;
    NTT(iva, N, -1);
    rec(i, n) b[i] = iva[i];
}

int inv[sid], ivf[sid], fac[sid];
inline void pre() {
    inv[0] = inv[1] = 1;
    fac[0] = fac[1] = 1;
    rep(i, 2, 200000) fac[i] = mul(fac[i - 1], i);
    rep(i, 2, 200000) inv[i] = mul(inv[mod % i], mod - mod / i);
    rep(i, 0, 200000) ivf[i] = fp(fac[i], mod - 2);
}

inline void wf(int *a, int *b, int n) { for(ri i = 1; i < n; i ++) b[i - 1] = mul(a[i], i); }
inline void jf(int *a, int *b, int n) { for(ri i = 1; i < n; i ++) b[i] = mul(a[i - 1], inv[i]); }

int ina[sid], inb[sid];
inline void In(int *a, int *b, int n) {
    int N = 1, lg = 0; init(n + n, N, lg);
    rec(i, N) ina[i] = inb[i] = 0;
    wf(a, ina, n); Inv(a, inb, n);
    rec(i, N) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (lg - 1));
    NTT(ina, N, 1); NTT(inb, N, 1);
    rec(i, N) ina[i] = mul(ina[i], inb[i]);
    NTT(ina, N, -1); jf(ina, b, n);
}

int exa[sid], exb[sid];
inline void Exp(int *a, int *b, int n) {
    if(n == 1) { b[0] = 1; return; }
    Exp(a, b, n >> 1);
    rec(i, n + n) exb[i] = exa[i] = 0;
    In(b, exb, n);
    int N = 1, lg = 0; init(n + n, N, lg);
    rec(i, N) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (lg - 1));
    rec(i, n) exa[i] = b[i], exb[i] = (a[i] - exb[i] + mod) % mod; exb[0] ++;
    NTT(exa, N, 1); NTT(exb, N, 1);
    rec(i, N) exa[i] = mul(exa[i], exb[i]);
    NTT(exa, N, -1);
    rec(i, n) b[i] = exa[i];
}

inline int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

int f[sid], g[sid];
inline void wish() {
    rep(i, 1, n) {
        if(vis[i]) continue;
        int L = 0;
        for(ri t = i; !vis[t]; t = p[t]) vis[t] = 1, L ++;
        nc[L] ++;
    }
    pre();
    int ret = 1;
    rep(i, 1, n) if(nc[i]) {
        int v = nc[i];
        rep(j, 0, v) f[j] = g[j] = 0;
        rep(j, 0, v) {
            if(gcd(j * i, n) != j) continue;
            f[j] = mul(mul(fac[j - 1], fp(i, j - 1)), ivf[j]);
        }
        int N = 1;
        while(N < v + 5) N <<= 1;
        Exp(f, g, N);
        ret = mul(ret, mul(g[v], fac[v]));
    }
    printf("%d\n", ret);
}

int main() {
    n = read();
    rep(i, 1, n) p[i] = read();
    wish();
    return 0;
}