【Python数据挖掘】回归模型与应用

线性回归 ( Linear Regression )

　　线性回归中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归称为一元线性回归。

　　如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归。

　　在监督学习中，学习样本为 D = { (x⁽ⁱ⁾, y⁽ⁱ⁾)；i =1, . . . , m } ，预测的结果y⁽ⁱ⁾为连续值变量，需要学习映射 f：X → Y ，并且假定输入X和输出Y之间有线性相关关系。

给出一组数据：

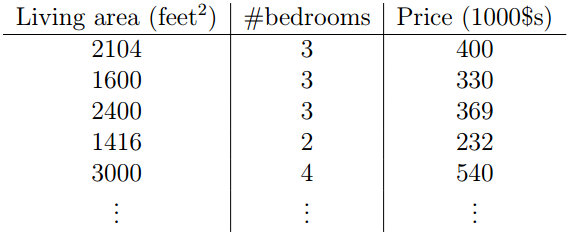
其中x是实数域中的二维向量。比如，xⁱ₁是第i个房子的居住面积，xⁱ₂是这个房子的房间数。

为了执行监督学习，我们需要决定怎样在计算机中表示我们的函数/假设。我们可以近似地使用线性函数来表示。

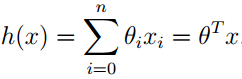（矩阵形式）

现在，有了训练数据，我们怎么挑选，或者说得知θ的值呢？一个可信的方法是使得h(x)与y更加接近，至少对于我们训练的例子来说是这样的。

于是，我们定义一个损失函数 / 成本函数( loss function / cost function )：

我们把 x 到 y 的映射函数 f 记作 θ 的函数 h_θ(x)

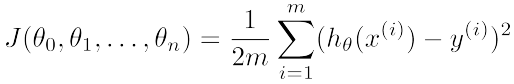
损失函数有很多种类型，根据需求进行选择。

然后进行最小化损失函数，将函数优化成凸函数 (往往只会有一个全局最优解，不用过多担心算法收敛到局部最优解) 。

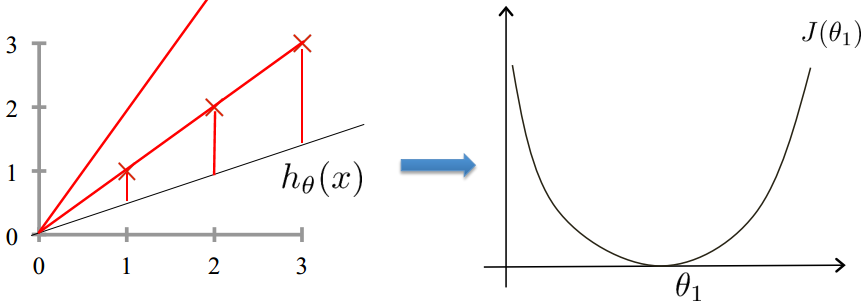
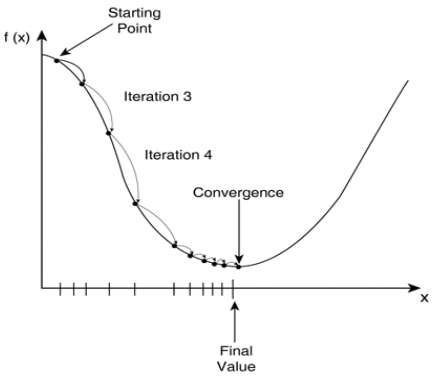
梯度下降 ( Gradient Descent algorithm )

　　最快的速度最小化损失函数，比作如何最快地下山，也就是每一步都应该往坡度最陡的方向往下走，而坡度最陡的方向就是损失函数相应的偏导数。

因此算法迭代的规则是：

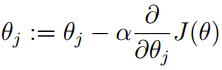
假设现在有n个特征、或者变量x_j(j=1…n)

其中α是算法的参数learning rate，α越大每一步下降的幅度越大，速度也会越快，但过大有可能反复震荡，导致算法不准确。

欠拟合与过拟合（Underfitting and Overfitting）

　　欠拟合问题：特征值少，模型过于简单不足与支撑。

　　过拟合问题：有非常多特征，模型很复杂, 我们的假设函数曲线可以对原始数据拟合得非常好，但丧失了一般性，从而导致对新给的待预测样本，预测效果差。

正则项、正则化

　　通过正则项控制参数幅度。

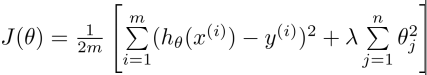
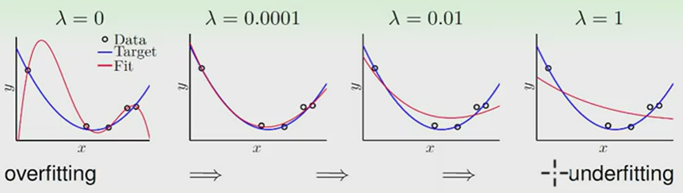
正则项有多种方式选择，常采用的有：

　　L1正则：|θ_j|

　　L2正则：θ_j²

Logistic 回归（Logistic Regression）

采用线性回归解决分类问题时，往往会遇到模型健壮性低，遇到噪声时，受干扰严重。

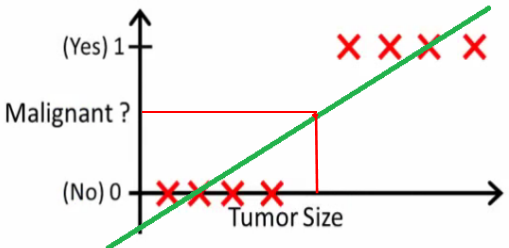
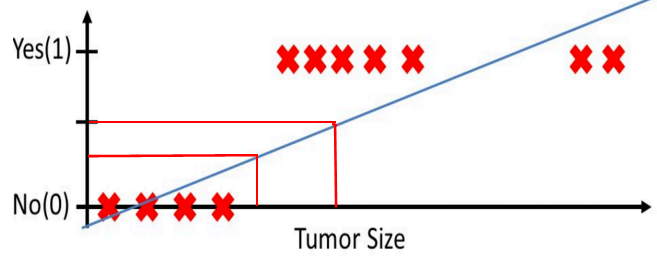
我们可以对旧的线性回归算法来进行适当的修改来得到我们想要的函数。

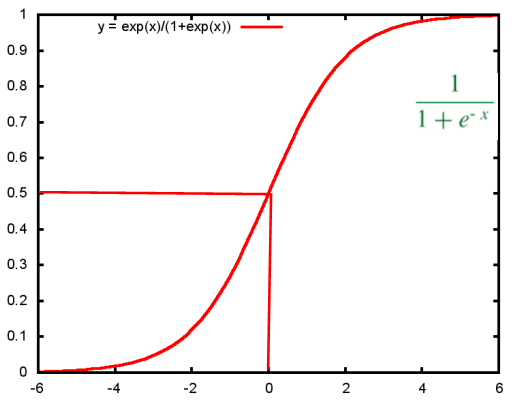
引入sigmoid 函数：

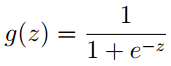
对原函数h_θ(x)进行改写得到：

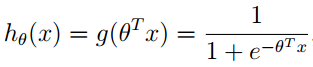
观察函数图像发现：当x大于0时，y的值大于0.5，根据这特性可以将线性回归得到的预测值压缩在0~1范围内。

1.线性判定边界：

假设线性函数为：，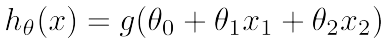

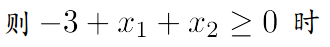
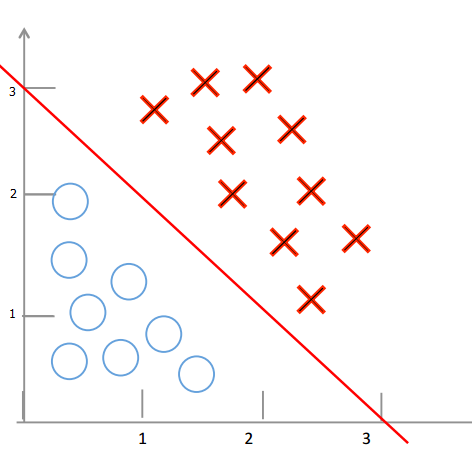
当 h_θ(x) > 0 时，g(h_θ(x)) 的值为大于 0.5；

当 h_θ(x) < 0 时，g(h_θ(x)) 的值为小于 0.5；

2.非线性判定边界：

假设函数为：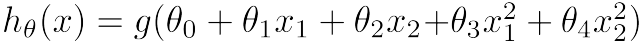

当θ₀=0，θ₁=0，θ₂=0，θ₃=1，θ₄=1，得到函数g(x₁²+x₂²-1)，边界为一个圆，圆内点的值小于0

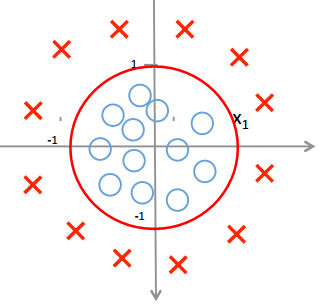
定义损失函数：

该函数为非凸函数，有局部最小值，应选择其他函数。

定义损失函数为：

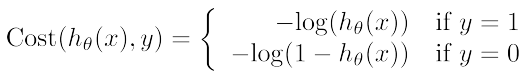
该函数的图像如下：

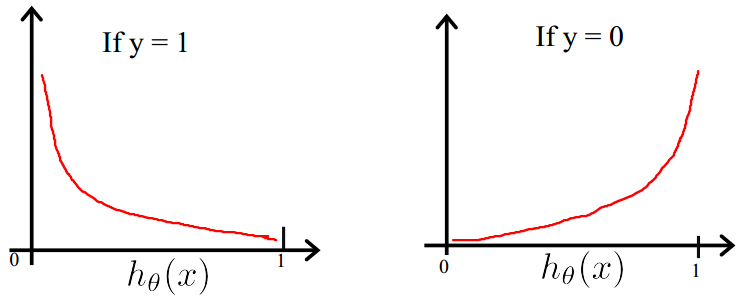
我们可以发现该函数在：

y=1的正样本中，h_θ(x)趋向于0.99~9 ，此时我们希望得到的代价越小，而当得到的预测值是0.00~1时，我们希望它的代价越大；

y=0的负样本中，h_θ(x)趋向于0.00~1 ，此时我们希望得到的代价越小，而当得到的预测值是0.99~9时，我们希望它的代价越大；

损失函数可以改写成：

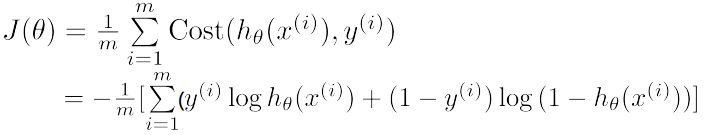
加入正则项：

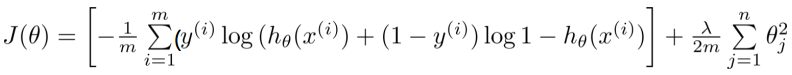
二分类与多分类

one vs one

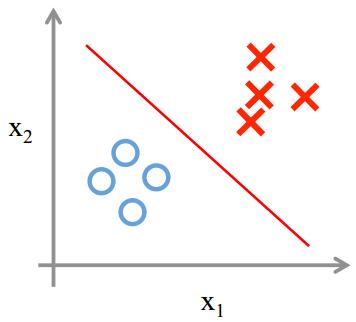
one vs rest

方法一：

1.先对三角形与叉叉进行分类，得到分类器C1，以及概率值P_c1(x) 和 1-P_c1(x)

2.然后对三角形与正方形进行分类，得到分类器C2，以及概率值P_c2(x) 和 1-P_c2(x)

3.最后对正方形与叉叉进行分类，得到分类器C3，以及概率值P_c3(x) 和 1-P_c3(x)

得到通过3个分类器,6个概率值，概率值最大的判断为相应的类型！

方法二：

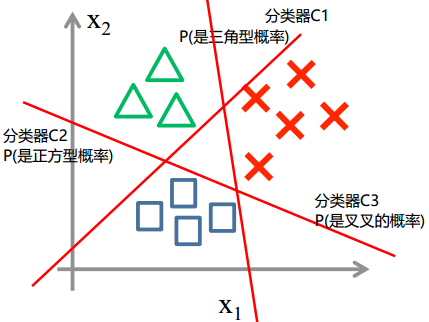
1.先对三角形进行分类，判断是否为三角形，得到分类器C1，以及概率值P_c1(x)

2.然后对正方形进行分类，判断是否为正方形，得到分类器C2，以及概率值P_c2(x)

3.最后对叉叉叉进行分类，判断是否为叉叉叉，得到分类器C3，以及概率值P_c3(x)

得到3个分类器，3个概率值，概率值最大的判断为相应的类型！

应用一：( Linear Regression )

1、导入相应的包，设置画图格式：

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

sns.set_context('notebook')

sns.set_style('white')

plt.figure(figsize=(8,6))

2、数据准备：