sklearn交叉验证3-【老鱼学sklearn】

在上一个博文中，我们用learning_curve函数来确定应该拥有多少的训练集能够达到效果，就像一个人进行学习时需要做多少题目就能拥有较好的考试成绩了。

本次我们来看下如何调整学习中的参数，类似一个人是在早上7点钟开始读书好还是晚上8点钟读书好。

加载数据

数据仍然利用手写数字识别作为训练数据：

from sklearn.datasets import load_digits

# 加载数据
digits = load_digits()
X = digits.data
y = digits.target

调整参数

我们想要调整·SVC(gamma=0.001)·SVC中的gamma参数，看到底把gamma参数设置成哪个值是最优的。

因此需要定义测试的参数范围，这里设置了参数值的范围为从10的-6次方到10的-2.3次方，总共5个值：

import numpy as np
# 定义gamma参数的可能取值范围，从10**-6, 到10**-2.3，总共5个参数值
param_range = np.logspace(-6, -2.3, 5)

用validation_curve不停尝试在不同参数值下的损失函数值：

from sklearn.model_selection import validation_curve
from sklearn.svm import SVC
# param_name中指定了修改SVC中的哪个参数值，这里修改的是gamma参数值；param_range参数指定了具体参数值的可选范围
train_loss, test_loss = validation_curve(SVC(), X, y, param_name="gamma", param_range=param_range, cv=10, scoring='neg_mean_squared_error')
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)

可视化图形

可视化图形，横坐标为参数可选值的范围，纵坐标为在各参数下的损失函数值

# 可视化图形，横坐标为参数可选值的范围，纵坐标为在各参数下的损失函数值
import matplotlib.pyplot as plt
plt.plot(param_range, train_loss_mean, label="Train")
plt.plot(param_range, test_loss_mean, label="Test")
plt.legend()
plt.show()

图形显示为：

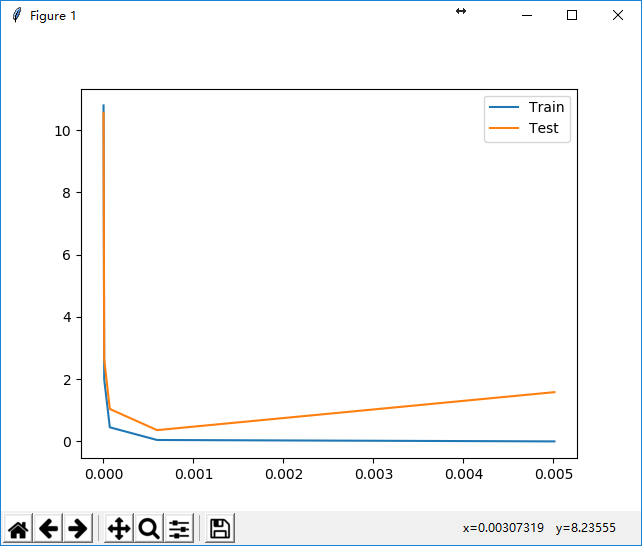
在这个图形中，我们发现gamma值有一个转折点，当其在0.001之后，测试集的误差值就开始扩大了，因此，从图形上看，一个比较好的学习参数值是gamma=0.001或者再往前一点点，大概在0.0007左右。

完整代码

完整的代码如下：

from sklearn.datasets import load_digits

# 加载数据
digits = load_digits()
X = digits.data
y = digits.target

import numpy as np
# 定义gamma参数的可能取值范围，从10**-6, 到10**-2.3，总共5个参数值
param_range = np.logspace(-6, -2.3, 5)

from sklearn.model_selection import validation_curve
from sklearn.svm import SVC
# param_name中指定了修改SVC中的哪个参数值，这里修改的是gamma参数值；param_range参数指定了具体参数值的可选范围
train_loss, test_loss = validation_curve(SVC(), X, y, param_name="gamma", param_range=param_range, cv=10, scoring='neg_mean_squared_error')
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)

# 可视化图形，横坐标为参数可选值的范围，纵坐标为在各参数下的损失函数值
import matplotlib.pyplot as plt
plt.plot(param_range, train_loss_mean, label="Train")
plt.plot(param_range, test_loss_mean, label="Test")
plt.legend()
plt.show()