Count on a tree SPOJ - COT （主席树，LCA）

You are given a tree with N nodes. The tree nodes are numbered from 1 to N. Each node has an integer weight.

We will ask you to perform the following operation:

u v k : ask for the kth minimum weight on the path from node u to node v

Input

In the first line there are two integers N and M. (N, M <= 100000)

In the second line there are N integers. The ith integer denotes the weight of the ith node.

In the next N-1 lines, each line contains two integers u v, which describes an edge (u, v).

In the next M lines, each line contains three integers u v k, which means an operation asking for the kth minimum weight on the path from node u to node v.

Output

For each operation, print its result.

Example

Input:

8 5

105 2 9 3 8 5 7 7

1 2

1 3

1 4

3 5

3 6

3 7

4 8
2 5 1
2 5 2
2 5 3
2 5 4
7 8 2

Output:

2
8
9
105
7 
给出一棵树，每个点都自己的权重，然后给出树上的边，要求从节点 u 到节点 v 路径上的第 k 小的权重的大小。
因为权重可能很大，所以需要离散化。
主席树求区间第 k 小维护的是权值线段树的前缀和，然后通过区间相减得到查询区间的权值线段树
所以树形结构的第 k 小维护的也是权值线段树的前缀和，这里的前缀和表示从第 i 个结点到根的前缀和，比如样例的树是

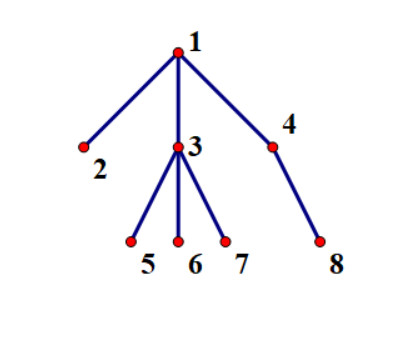
那么我们用主席树把这八个结点维护成这个样子

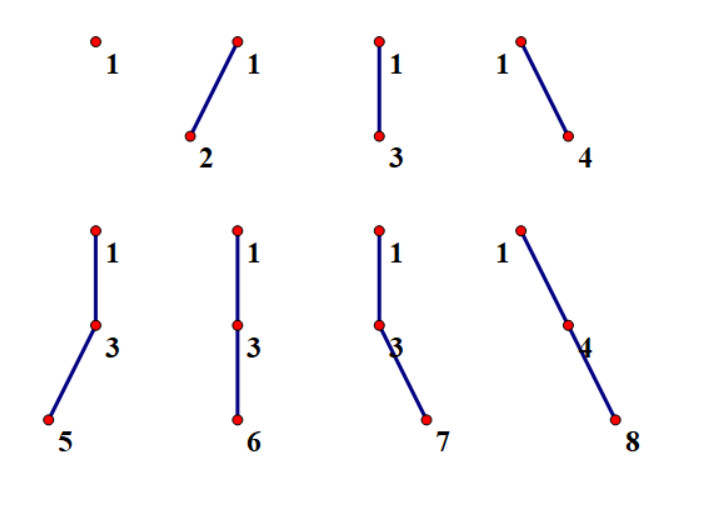
那么要得到其中两个点（u，v）之间的树形结构，就可以看成 TREE（u） + TREE（v） - TREE（lca（u，v））- TREE（fa（lca（u，v））），把查询看成四棵树之间的相加相减，然后在求一下lca（u，v）就可以了，这里我比较懒直接用在线的写了

 /*

           .

          ';;;;;.

         '!;;;;;;!;`

        '!;|&#@|;;;;!:

       `;;!&####@|;;;;!:

      .;;;!&@$$%|!;;;;;;!'.`:::::'.

      '!;;;;;;;;!$@###&|;;|%!;!$|;;;;|&&;.

      :!;;;;!$@&%|;;;;;;;;;|!::!!:::;!$%;!$%`    '!%&#########@$!:.

      ;!;;!!;;;;;|$$&@##$;;;::'''''::;;;;|&|%@$|;;;;;;;;;;;;;;;;!$;

      ;|;;;;;;;;;;;;;;;;;;!%@#####&!:::;!;;;;;;;;;;!&####@%!;;;;$%`

     `!!;;;;;;;;;;!|%%|!!;::;;|@##%|$|;;;;;;;;;;;;!|%$#####%;;;%&;

     :@###&!:;;!!||%%%%%|!;;;;;||;;;;||!$&&@@%;;;;;;;|$$##$;;;%@|

     ;|::;;;;;;;;;;;;|&&$|;;!$@&$!;;;;!;;;;;;;;;;;;;;;;!%|;;;%@%.

    `!!;;;;;;;!!!!;;;;;$@@@&&&&&@$!;!%|;;;;!||!;;;;;!|%%%!;;%@|.

 %&&$!;;;;;!;;;;;;;;;;;|$&&&&&&&&&@@%!%%;!||!;;;;;;;;;;;;;$##!

 !%;;;;;;!%!:;;;;;;;;;;!$&&&&&&&&&&@##&%|||;;;!!||!;;;;;;;$&:

 ':|@###%;:;;;;;;;;;;;;!%$&&&&&&@@$!;;;;;;;!!!;;;;;%&!;;|&%.

  !@|;;;;;;;;;;;;;;;;;;|%|$&&$%&&|;;;;;;;;;;;;!;;;;;!&@@&'

   .:%#&!;;;;;;;;;;;;;;!%|$$%%&@%;;;;;;;;;;;;;;;;;;;!&@:

   .%$;;;;;;;;;;;;;;;;;;|$$$$@&|;;;;;;;;;;;;;;;;;;;;%@%.

     !&!;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;|@#;

      `%$!;;;;;;;;;;;$@|;;;;;;;;;;;;;;;;;;;;;;;;!%$@#@|.

        .|@%!;;;;;;;;;!$&%||;;;;;;;;;;;;;;;;;!%$$$$$@#|.

            ;&$!;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;%#####|.

            |##$|!;;;;;;::'':;;;;;;;;;;;;;!%$$$@#@;

           ;@&|;;;;;;;::'''''':;;;;;;;|$&@###@|`

         .%##@|;;;;:::''''''''''::;!%&##$'

       `$##@$$@@&|!!;;;:'''''::::;;;;;|&#%.

     ;&@##&$%!;;;;;;::''''''''::;!|%$@#@&@@:

      .%@&$$|;;;;;;;;;;:'''':''''::;;;%@#@@#%.

     :@##@###@$$$$$|;;:'''':;;!!;;;;;;!$#@@#$;`

      `%@$$|;;;;;;;;:'''''''::;;;;|%$$|!!&###&'

      |##&%!;;;;;::''''''''''''::;;;;;;;!$@&:`!'

     :;!@$|;;;;;;;::''''''''''':;;;;;;;;!%&@$:                !@#$'

       |##@@&%;;;;;::''''''''':;;;;;;;!%&@#@$%:            '%%!%&;

       |&%!;;;;;;;%$!:''''''':|%!;;;;;;;;|&@%||`         '%$|!%&;

       |@%!;;!!;;;||;:'''''':;%$!;;;;!%%%&#&%$&:        .|%;:!&%`

       !@&%;;;;;;;||;;;:''::;;%$!;;;;;;;|&@%;!$;       `%&%!!$&:

       '$$|;!!!!;;||;;;;;;;;;;%%;;;;;;;|@@|!$##;      !$!;:!$&:

        |#&|;;;;;;!||;;;;;;;;!%|;;;;!$##$;;;;|%'   `%$|%%;|&$'

         |&%!;;;;;;|%;;;;;;;;$$;;;;;;|&&|!|%&&;  .:%&$!;;;:!$@!

         `%#&%!!;;;;||;;;;;!$&|;;;!%%%@&!;;;!!;;;|%!;;%@$!%@!

         !&!;;;;;;;;;||;;%&!;;;;;;;;;%@&!;;!&$;;;|&%;;;%@%`

        '%|;;;;;;;;!!|$|%&%;;;;;;;;;;|&#&|!!||!!|%$@@|'

        .!%%&%'`|$;     :|$#%|@#&;%#%.

 */

 #include <map>

 #include <set>

 #include <list>

 #include <ctime>

 #include <cmath>

 #include <stack>

 #include <queue>

 #include <string>

 #include <vector>

 #include <cstdio>

 #include <bitset>

 #include <cstdlib>

 #include <cstring>

 #include <iostream>

 #include <algorithm>

 #define  lowbit(x)  x & (-x)

 #define  mes(a, b)  memset(a, b, sizeof a)

 #define  fi         first

 #define  se         second

 #define  pii        pair<int, int>

 #define  INOPEN     freopen("in.txt", "r", stdin)

 #define  OUTOPEN    freopen("out.txt", "w", stdout)

 typedef unsigned long long int ull;

 typedef long long int ll;

 const int    maxn = 1e5 + ;

 const int    maxm = 1e5 + ;

 const int    mod  = 1e9 + ;

 const ll     INF  = 1e18 + ;

 const int    inf  = 0x3f3f3f3f;

 const double pi   = acos(-1.0);

 const double eps  = 1e-;

 using namespace std;

 int n, m;

 int cas, tol, T;

 struct Node {

     int l, r;

     int sum;

 } node[maxn * ];

 int a[maxn];

 int rt[maxn];

 bool vis[maxn];

 int deep[maxn];

 int fa[maxn][];

 vector<int> vec[maxn];

 vector<int> vv;

 void init() {

     tol = ;

     mes(a, );

     mes(rt, );

     mes(fa, );

     mes(vis, );

     mes(node, );

     mes(deep, );

     vv.clear();

     for(int i=; i<=n; i++)

         vec[i].clear();

 }

 int getid(int x) {

     return lower_bound(vv.begin(), vv.end(), x) - vv.begin() + ;

 }

 void lca_dfs(int u, int f, int d) {

     deep[u] = d;

     int len = vec[u].size();

     for(int i=; i<len; i++) {

         int v = vec[u][i];

         if(v == f)    continue;

         if(fa[v][])continue;

         fa[v][] = u;

         lca_dfs(v, u, d+);

     }

 }

 void lca_update() {

     for(int j=; (<<j)<=n; j++) {

         for(int i=; i<=n; i++) {

             fa[i][j] = fa[fa[i][j-]][j-];

         }

     }

 }

 int lca_query(int u, int v) {

     if(deep[u] < deep[v])    swap(u, v);

     int f = deep[u] - deep[v];

     for(int i=; (<<i)<=f; i++) {

         if(f & (<<i)) {

             u = fa[u][i];

         }

     }

     if(u != v) {

         for(int i=(int)log2(n); i>=; i--) {

             if(fa[u][i] != fa[v][i]) {

                 u = fa[u][i];

                 v = fa[v][i];

             }

         }

         u = fa[u][];

     }

     return u;

 }

 void hjt_update(int l, int r, int &x, int y, int pos) {

     tol++;

     node[tol] = node[y];

     node[tol].sum++;

     x = tol;

     if(l == r)    return ;

     int mid = (l + r) >> ;

     if(pos <= mid)

         hjt_update(l, mid, node[x].l, node[y].l, pos);

     else

         hjt_update(mid+, r, node[x].r, node[y].r, pos);

 }

 void hjt_build(int u, int f) {

 //    printf("%d %d\n", u, f);

     hjt_update(, n, rt[u], rt[f], getid(a[u]));

     vis[u] = true;

     int len = vec[u].size();

     for(int i=; i<len; i++) {

         int v = vec[u][i];

         if(vis[v])    continue;

         if(v == f)    continue;

         hjt_build(v, u);

     }

 }

 int hjt_query(int l, int r, int x, int y, int lca, int flca, int k) {

     if(l == r)

         return l;

     int mid = (l + r) >> ;

     int sum = node[node[x].l].sum + node[node[y].l].sum - node[node[lca].l].sum - node[node[flca].l].sum;

     if(k <= sum)

         return hjt_query(l, mid, node[x].l, node[y].l, node[lca].l, node[flca].l, k);

     else

         return hjt_query(mid+, r, node[x].r, node[y].r, node[lca].r, node[flca].r, k-sum);

 }

 int main() {

     scanf("%d%d", &n, &m);

     init();

     for(int i=; i<=n; i++) {

         scanf("%d", &a[i]);

         vv.push_back(a[i]);

     }

     sort(vv.begin(), vv.end());

     vv.erase(unique(vv.begin(), vv.end()), vv.end());

     for(int i=; i<n; i++) {

         int u, v;

         scanf("%d%d", &u, &v);

         vec[u].push_back(v);

         vec[v].push_back(u);

     }

     fa[][] = ;

     lca_dfs(, , );

     lca_update();

     hjt_build(, );

     while(m--) {

         int u, v, k;

         scanf("%d%d%d", &u, &v, &k);

         int ans = hjt_query(, n, rt[u], rt[v], rt[lca_query(u, v)], rt[fa[lca_query(u, v)][]], k);

         printf("%d\n", vv[ans-]);

     }

     return ;

 }