CF145E Lucky Queries 题解

题目链接：CF 或者洛谷

前置知识点：序列操作

本文关键词约定俗称：因为频繁敲最长不下降子序列 $LNCS$ 和最长不上升子序列 $LNIS$ 太麻烦了，下文将 $000011111$ 这种最长不降子序列用 $LIS$ 描述，$1111100000$ 这种最长不升子序列用 $LDS$ 描述。

这里面只有 $4$ 和 $7$，抽象当做 $0$ 和 $1$，那么那个交换两种数操作其实就是区间取反操作，接下来解决如何维护区间的 $01序列LIS$ 问题。$01$ 序列比较特别，它的 $LIS$ 一定是类似于 $00001111$ 这样的形式，其中 $0$ 与 $1$ 的个数都可以为 $0$。如果做过维护最大子段和问题的很容易想到这类问题，其实也可以由局部的最大子段和进行拼段得到新的区间上的最大子段和。

难点讲解

如何在线段树上的 pushUp 中去进行计算 $LIS$。

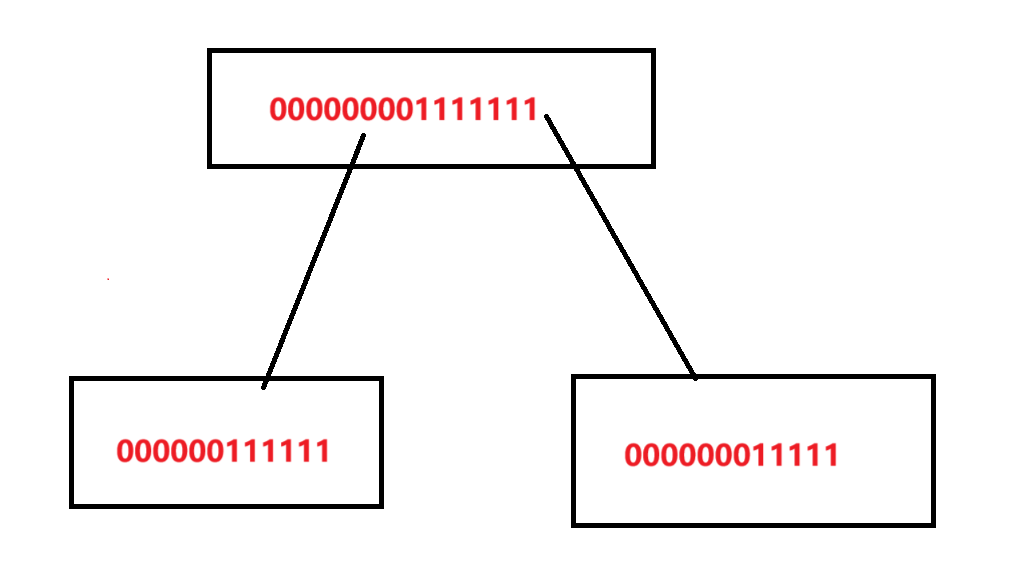
如图所示，具体数字数值不做参考，如果我们已经知道了两个节点区间表示的 $LIS$，容易知道如果是左边的 $LIS$，那么一定要加上右边的 $1$ 的个数才能拼成新的 $LIS$，右边的 $LIS$ 一定需要加上左边的 $0$ 的个数才能组成父节点的 $LIS$。那么考虑二者中最大的一定是父节点的 $LIS$ 吗？

证明：

先考虑一个特殊情况是否也满足，假如它的 $LIS$ 为全 $1$ 或者全 $0$。容易发现，如果左边节点为全 $0$，那么在右边的 $LIS$ 拼左边的 $0$ 的个数的时候，就能涵盖了这种情况。

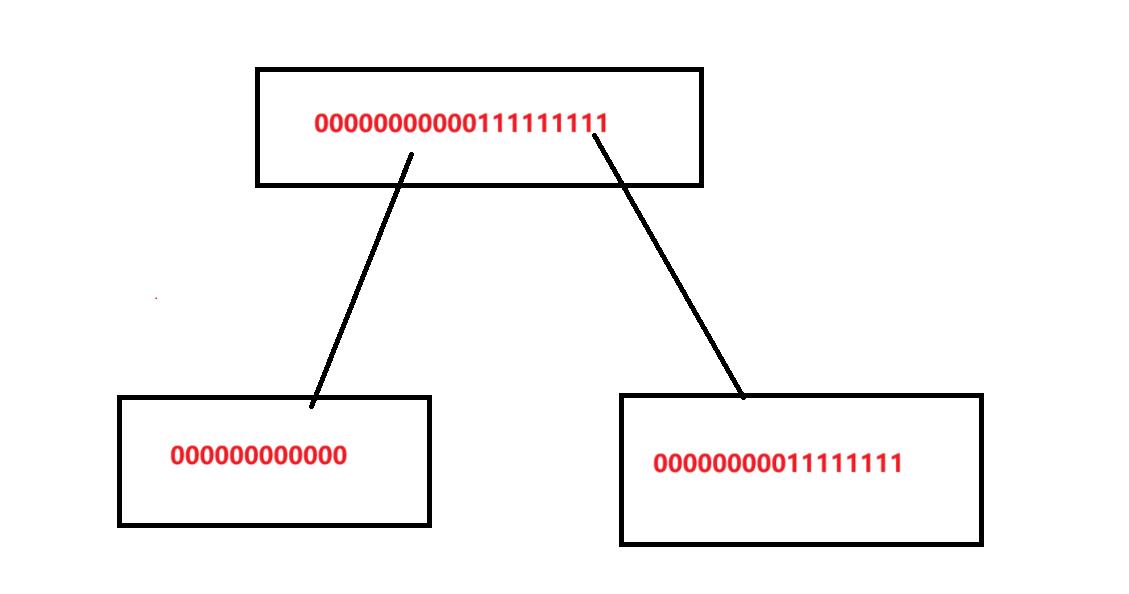
全 $1$ 也是同理的。那么也就是说这类的特殊情况是被包括在我们讨论的 $0000011111$ 这种连续段中的，并不会影响，即 $0$ 或者 $1$ 的个数为 $0$ 并不影响讨论。

考虑全局 $LIS$ 的特点，对于父节点的 $LIS$ 一定也是长 $0000011111$ 这样子的，并且一定有一个分割点 $mid$ 使得这个 $01$ 串分割为两部分，左半边为左区间的子序列，右半边为右区间的子序列，当然，这个子序列长度也可恶意为 $0$，比如：

$[1,5]$ 区间，它的串表示为 $11100$，其中 $[1,3]$ 的串为 $111$，$[4,5]$ 的串为 $00$，而 $[1,5]$ 的 $LIS$ 为 $111$，显然我们这个 $mid$ 该放在最后一个 $1$ 的后面，前面的 $111$ 为左半区间，后面的 “空串” 为右半区间的子序列。

那么我们来考虑 $mid$ 除开特殊的空串情况以外的可能情况，其实空串也被包括在了上述说的全 $1$ 或者全 $0$ 的特殊情况中了。

$mid$ 放在了某个 $0$ 上，那么将原串分割为 $000$ 与 $000011111$，前者为左区间的串，显然最优为 $LIS$ 时，应该取 $0$ 的数量，后面要求 $01$ 串这种连续串最长，显而易见是右区间的 $LIS$。符合我们说的其中一个情况：$Zero_{left}+LIS_{right}$。
$mid$ 放在某个 $1$ 上，那么同上分析分割为了 $0001111$ 与 $11111$，显然最优的 $LIS$ 时为：$LIS_{left}+One_{right}$。

综上所述，$LIS$ 的所有情况是被上述两种情况给包含了的，我们并没有遗漏情况。

0-1串 LIS 带翻转操作

现在这玩意带上翻转操作咋整，看到前置知识点那题没，其实 $0-1 串$ 是一个非常好的问题结构，它的取反会得到一个对偶问题：$LDS$ 最长不增序列，即 $111111000000$，类似于前置知识点问题，我们同时类似维护它的对偶问题的的答案，翻转即是两个问题的答案互换即可。读者可以先写写前置知识点的那题，可以先学习我的那篇题解再进行本题观摩就很容易懂了对偶问题的答案互换的意思了。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)

// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")

// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/tree_policy.hpp>

#include <ext/pb_ds/trie_policy.hpp>

#include <ext/pb_ds/tag_and_trait.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/list_update_policy.hpp>

#include <ext/pb_ds/assoc_container.hpp>

#include <ext/pb_ds/exception.hpp>

#include <ext/rope>

#endif

using namespace std;

using namespace __gnu_cxx;

using namespace __gnu_pbds;

typedef long long ll;

typedef long double ld;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

typedef tuple<int, int, int> tii;

typedef tuple<ll, ll, ll> tll;

typedef unsigned int ui;

typedef unsigned long long ull;

typedef __int128 i128;

#define hash1 unordered_map

#define hash2 gp_hash_table

#define hash3 cc_hash_table

#define stdHeap std::priority_queue

#define pbdsHeap __gnu_pbds::priority_queue

#define sortArr(a, n) sort(a+1,a+n+1)

#define all(v) v.begin(),v.end()

#define yes cout<<"YES"

#define no cout<<"NO"

#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);

#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);

#define forn(i, a, b) for(int i = a; i <= b; i++)

#define forv(i, a, b) for(int i=a;i>=b;i--)

#define ls(x) (x<<1)

#define rs(x) (x<<1|1)

#define endl '\n'

//用于Miller-Rabin

[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>

int disc(T* a, int n)

{

    return unique(a + 1, a + n + 1) - (a + 1);

}

template <typename T>

T lowBit(T x)

{

    return x & -x;

}

template <typename T>

T Rand(T l, T r)

{

    static mt19937 Rand(time(nullptr));

    uniform_int_distribution<T> dis(l, r);

    return dis(Rand);

}

template <typename T1, typename T2>

T1 modt(T1 a, T2 b)

{

    return (a % b + b) % b;

}

template <typename T1, typename T2, typename T3>

T1 qPow(T1 a, T2 b, T3 c)

{

    a %= c;

    T1 ans = 1;

    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;

    return modt(ans, c);

}

template <typename T>

void read(T& x)

{

    x = 0;

    T sign = 1;

    char ch = getchar();

    while (!isdigit(ch))

    {

        if (ch == '-')sign = -1;

        ch = getchar();

    }

    while (isdigit(ch))

    {

        x = (x << 3) + (x << 1) + (ch ^ 48);

        ch = getchar();

    }

    x *= sign;

}

template <typename T, typename... U>

void read(T& x, U&... y)

{

    read(x);

    read(y...);

}

template <typename T>

void write(T x)

{

    if (typeid(x) == typeid(char))return;

    if (x < 0)x = -x, putchar('-');

    if (x > 9)write(x / 10);

    putchar(x % 10 ^ 48);

}

template <typename C, typename T, typename... U>

void write(C c, T x, U... y)

{

    write(x), putchar(c);

    write(c, y...);

}

template <typename T11, typename T22, typename T33>

struct T3

{

    T11 one;

    T22 tow;

    T33 three;

    bool operator<(const T3 other) const

    {

        if (one == other.one)

        {

            if (tow == other.tow)return three < other.three;

            return tow < other.tow;

        }

        return one < other.one;

    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)

    {

    }

};

template <typename T1, typename T2>

void uMax(T1& x, T2 y)

{

    if (x < y)x = y;

}

template <typename T1, typename T2>

void uMin(T1& x, T2 y)

{

    if (x > y)x = y;

}

constexpr int N = 1e6 + 10;

struct Node

{

    int sum4, sum7, LIS, LDS;

    int rev, len;

} node[N << 2];

#define sum4(x) node[x].sum4

#define sum7(x) node[x].sum7

#define LIS(x) node[x].LIS

#define LDS(x) node[x].LDS

#define len(x) node[x].len

#define rev(x) node[x].rev

inline void push_up(const int curr)

{

    sum4(curr) = sum4(ls(curr)) + sum4(rs(curr));

    sum7(curr) = sum7(ls(curr)) + sum7(rs(curr));

    LIS(curr) = max(LIS(ls(curr)) + sum7(rs(curr)),sum4(ls(curr)) + LIS(rs(curr)));

    LDS(curr) = max(LDS(ls(curr)) + sum4(rs(curr)),sum7(ls(curr)) + LDS(rs(curr)));

}

inline void RevTag(const int curr)

{

    sum4(curr) = len(curr) - sum4(curr);

    sum7(curr) = len(curr) - sum7(curr);

    swap(LIS(curr),LDS(curr));

    rev(curr) ^= 1;

}

inline void push_down(const int curr)

{

    if (rev(curr))

    {

        RevTag(ls(curr)), RevTag(rs(curr));

        rev(curr) = 0;

    }

}

int n, q;

char a[N];

inline void build(const int curr = 1, const int l = 1, const int r = n)

{

    len(curr) = r - l + 1;

    const int mid = l + r >> 1;

    if (l == r)

    {

        LIS(curr) = LDS(curr) = 1;

        sum4(curr) = a[l] == '4';

        sum7(curr) = a[l] == '7';

        return;

    }

    build(ls(curr), l, mid);

    build(rs(curr), mid + 1, r);

    push_up(curr);

}

inline void Rev(const int curr, const int l, const int r, const int s = 1, const int e = n)

{

    if (l <= s and e <= r)

    {

        RevTag(curr);

        return;

    }

    const int mid = s + e >> 1;

    push_down(curr);

    if (l <= mid)Rev(ls(curr), l, r, s, mid);

    if (r > mid)Rev(rs(curr), l, r, mid + 1, e);

    push_up(curr);

}

string s;

inline void solve()

{

    cin >> n >> q;

    forn(i, 1, n)cin >> a[i];

    build();

    while (q--)

    {

        cin >> s;

        if (s == "count")cout << LIS(1) << endl;

        else

        {

            int l, r;

            cin >> l >> r;

            Rev(1, l, r);

        }

    }

}

signed int main()

{

    // MyFile

    Spider

    //------------------------------------------------------

    // clock_t start = clock();

    int test = 1;

    //    read(test);

    // cin >> test;

    forn(i, 1, test)solve();

    //    while (cin >> n, n)solve();

    //    while (cin >> test)solve();

    // clock_t end = clock();

    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;

}

\[时间复杂度为：\ O(q\log{n})
\]