【洛谷】P4139 上帝与集合的正确用法

题目描述

根据一些书上的记载，上帝的一次失败的创世经历是这样的：
  第一天，上帝创造了一个世界的基本元素，称做“元”。
  第二天，上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。
  第三天，上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。
  第四天，上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。
  如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。
  然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……
  然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。
  至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？
  上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。
  你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。
  一句话题意

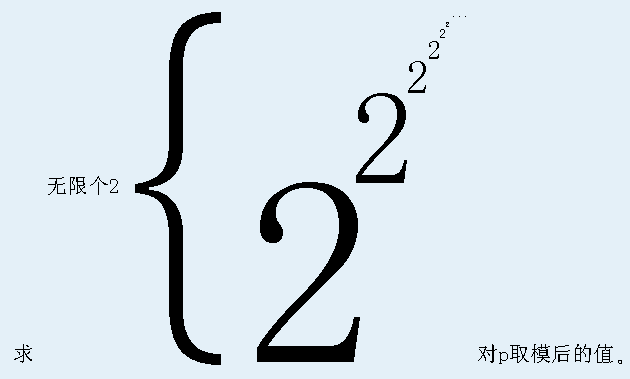
输入格式

多组数据，先输入一个整数T，接下来T行，每行一个正整数p，代表你需要取模的值。

输出格式

T行，每行一个正整数，为答案对p取模后的值
输入样例
  3
  2
  3
  6
输出样例
  0
  1
  4
提示
  对于100%的数据，T<=1000,p<=10^7

分析

做这题第一眼还想用mod-2，然后发现p不是质数而且还不会写。。。。。。

索性直接看题解，滚去学了一下欧拉定理和扩展欧拉定理

对于不互质的两个数a与b有以下关系

$$a^{k}\equiv a^{k\%{\varphi (b)}+\varphi (b)}(mod \ b)$$

所以直接对指数递归下去做就好，模数因为是取欧拉函数所以肯定递减，模数减到1的时候就可以直接返回0了

Code

#include<cstdio>
int T;
int phi(int x)
{
    int ans=x;
    for(int i=;1ll*i*i<=x;i++)
    if(x%i==){ans=ans/i*(i-);while(x%i==)x/=i;}
    if(x!=)ans=ans/x*(x-);
    return ans;
}
int qp(int a,int k,int p)
{
    int res=;
    while(k)
    {
        if(k&)res=1ll*a*res%p;
        a=1ll*a*a%p;k>>=;
    }
    return res;
}
int solve(int p)
{
    if(p==)return ;
    int x=phi(p);
    return qp(,solve(x)+x,p);
}
int main()
{
    scanf("%d",&T);
    for(int t=,p;t<=T;t++)
    scanf("%d",&p),printf("%d\n",solve(p));
}