【16.56%】【codeforces 687B】Remainders Game

time limit per test1 second

memory limit per test256 megabytes

inputstandard input

outputstandard output

Today Pari and Arya are playing a game called Remainders.

Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 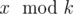. There are n ancient numbers c1, c2, …, cn and Pari has to tell Arya 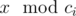if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 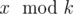for any positive integer x?

Note, that 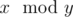means the remainder of x after dividing it by y.

Input

The first line of the input contains two integers n and k (1 ≤ n,  k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.

The second line contains n integers c1, c2, …, cn (1 ≤ ci ≤ 1 000 000).

Output

Print “Yes” (without quotes) if Arya has a winning strategy independent of value of x, or “No” (without quotes) otherwise.

Examples

input

4 5

2 3 5 12

output

Yes

input

2 7

2 3

output

No

Note

In the first sample, Arya can understand 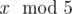because 5 is one of the ancient numbers.

In the second sample, Arya can’t be sure what 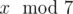is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.

【题解】



题意:

让你猜x % k 的值

但是只告诉你k以及一系列x % ci;

做法:

根据中国剩余定理:

如果知道了

x % a;

x % b;

x % c;

x % d;

····

且a,b,c,d互质;

那么x % (abcd)就可以确定了;

那么因为要求x % k

所以对k进行质数分解;

各个质数肯定是互质的；

分解成k = p1^k1*p2^k2…pn^kn的形式

然后你还得知道这么一个东西

如果

a 是 b的倍数，即a %b==0

那么

x % a = y1

x % b = y2

那么y2 = y1 % b;

即

x = t1*a+ y1 ···①

x = t2*b + y2

因为a是b的倍数

所以①式总可以写成

x = t1*t3*b + y1的形式

显然y1 再对b取模就是y2了；

回到质数分解后

分解成k = p1^k1*p2^k2…pn^kn的形式

我们想知道

x % p1^k1

x % p2^k2

….

x % pn^kn

这样我们就能知道x %k了

根据上面的分析，我们只要在所给的ci里面找pi^ki的倍数就好了；

如果对于所有的t∈[1..n]总有数字ci是pt^kt的倍数;

因为如果ci是pt^kt的倍数,则x % ci知道了，相应的x%(pt^kt)按照上面的分析也能知道了->(x%ci) % (pt^kt)

既然知道了所有的x%pt^kt

那么就能求出x%k了；

#include <cstdio>

int n, k,cnt = 0;
int num[10000];
bool cover[10000] = { 0 };

int main()
{
    //freopen("F:\\rush.txt", "r", stdin);
    scanf("%d%d", &n, &k);
    for (int i = 2;i <= k;i++)
        if ((k%i) == 0)
        {
            int now = 1;
            while ((k%i) == 0)
            {
                now = now*i;
                k /= i;
            }
            num[++cnt] = now;//存的是p1^k1..pcnt^kcnt
        }
    for (int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        for (int j = 1; j <= cnt; j++)
            if (x % num[j] == 0)//如果是的x%pt^kt倍数,那么x%pt^kt就能求出来了
                cover[j] = true;
    }
    for (int j = 1;j <= cnt;j++)
        if (!cover[j])
        {
            puts("NO");
            return 0;
        }
    puts("YES");
    return 0;
}