理解"熵"

熵描述了事物的混乱程度

一个变量x,它的可取值为x1,x2,x3,x4.当它取值为这几个值时,概率分别为p1,p2,p3,p4.那么这个混乱程度就可以描述为f(p1,p2,p3,p4).

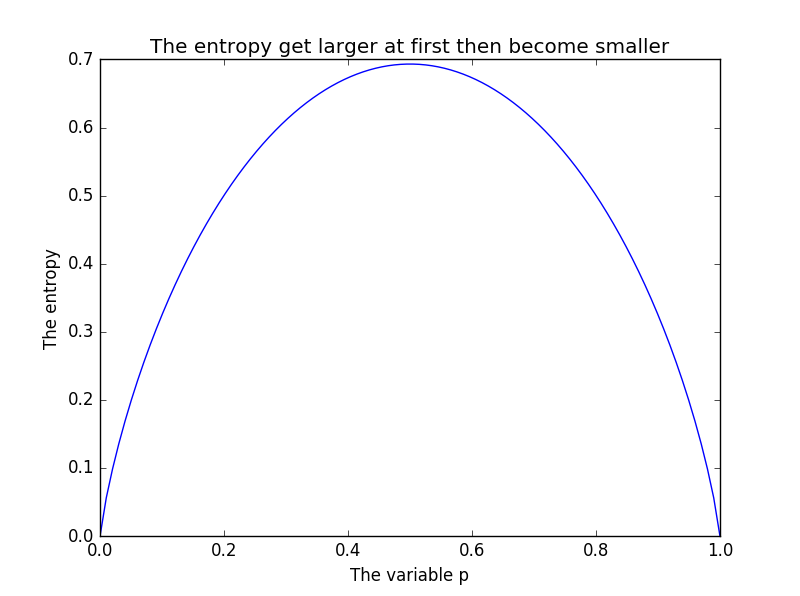
二元取值时熵随p1的变化

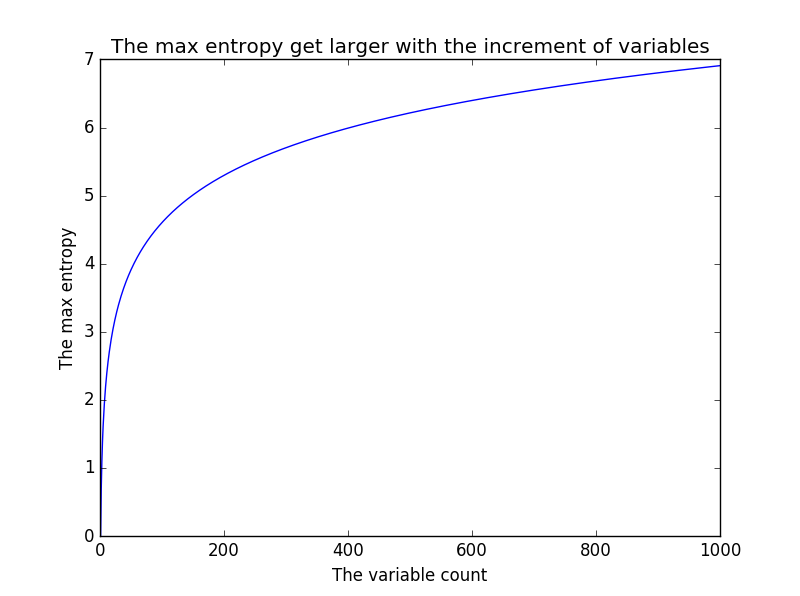
随着可取值个数的增加,熵的最大值逐渐增大

熵的最大值在各个变量概率相等的情况下取得,也就是说,越是等概率的取值,混乱程度越大.
f(x)=x*[-(1/x)*ln(1/x)]=-ln(1/x)=ln(x)

熵的另一种描述----基尼系数

基尼系数定义为：对于变量x，取两次，得到x1和x2，他们不相等的概率就是系统的熵！
多么简洁明了的定义，从概率的角度出发进行定义熵。
和香农熵一样，基尼系数也描述了系统的混乱程度。
那么基尼系数如何计算呢？用逆向思维：求x1=x2的概率，即p1^2+p2^2+p3^2。。。,基尼系数=1-p（x1=x2）=1-p1*p1-p2*p2-p3*p3。
很容易想到，基尼系数的图像类似二次函数的图像。

画出上面两幅图的代码

import matplotlib.pyplot as plt
import numpy as np
import math

x = np.linspace(0.00001, 0.999999, 100)
y = -(x * np.log(x) + (1 - x) * np.log(1 - x))
plt.plot(x, y)
plt.title('The entropy get larger at first then become smaller')
plt.xlabel('The variable p')
plt.ylabel('The entropy')
plt.show()

varCount=1000
vars=list(range(1,varCount))
maxEntropy = [i * (-1 / i * math.log(1 / i)) for i in vars]
plt.plot(vars,maxEntropy)
plt.title("The max entropy get larger with the increment of variables")
plt.xlabel("The variable count")
plt.ylabel("The max entropy")
plt.show()