Note: Bimodal Content Defined Chunking for Backup Streams

CDC算法给出了一个chunk的大小的最小值、最大值、平均值的界定。

Method

Using chunk existence information

breaking-apart algorithm

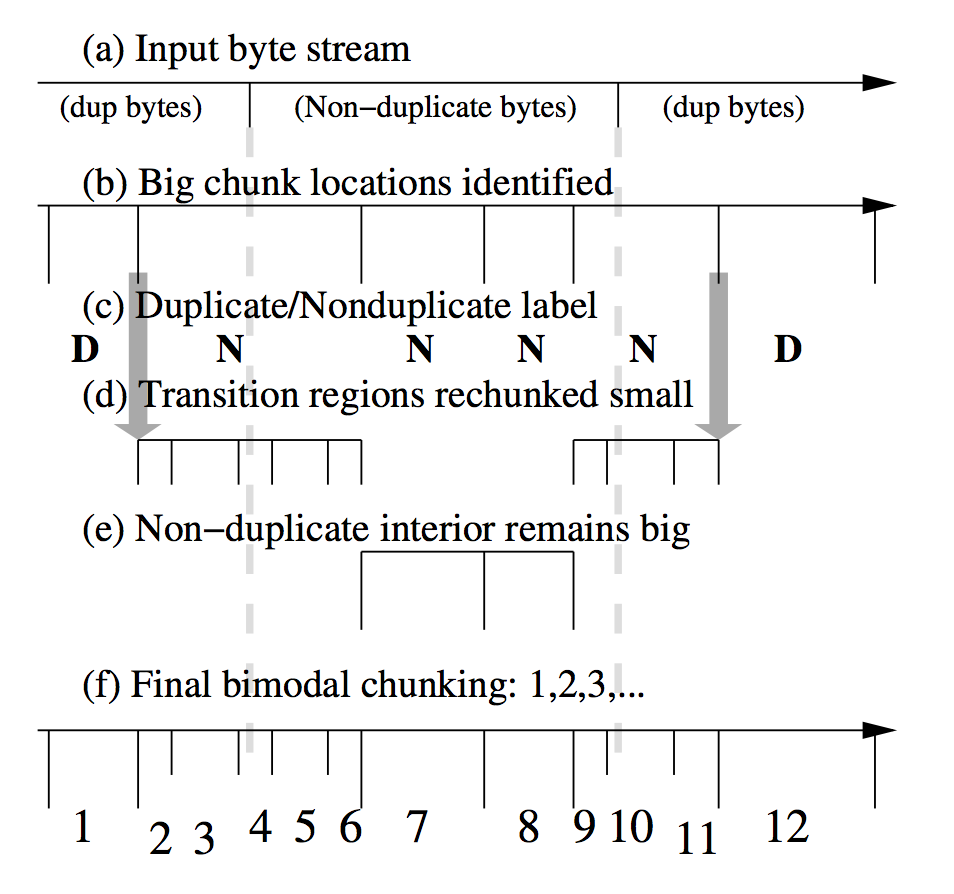
将所有内容全部划分为较大的chunk，然后识别新内容的变化区域，然后在这个变化区域的附近重新划分较小的chunk。重复进行数据重删。

building-up algorithm

在开始时将chunk的大小初始化为一个较为合适的值，然后组合较小的chunk。通过一个建块算法，查询更多的大块的位置和更细小的单个插入修改块。在输入中的任意位置均需要判断要建立小块还是建立大块，这种算法称之为bimodal chunking算法。

Baseline rolling window cut-point selection.

与预设值匹配给定的l个bit的值，如果匹配成功，则在l bit的最后一位处产生了切割点。几何分布下定义平均chunk大小为\(2^l\)。将其称为\(level-2^l\)chunker。

对于chunk最小值\(m\)，通常chunk的平均大小是\(m+2^l\)。对于chunk最大值\(M\)，一个\(level-2^l\) chunker通常会达到最大值：\(e^{-(M-m)/2^l}\)。在这里，M并非内容定义的。对于备份数据，给出\(level-2^{l-b}\) chunk，尽量避免非文本定义的切割点。

Breaking-apart algorithms



Chunk amalgamation algorithms

resynchronization 再同步