连续bezier曲线的实现

需求场景

一系列的坐标点，划出一条平滑的曲线

3次Bezier曲线

基本上大部分绘图工具都实现了3次Bezier曲线，4个点确定一条3次Bezier曲线。以html5中的canvas为例

let ctx = canvas.getContex('2d');
ctx.moveTo(20,20); // 曲线起点 Fom
ctx.bezierCurveTo(20,100,200,100,200,20); // 分别为控制点 Ctrl1,Ctrl2, 终点 To

连续Bezier曲线

假定给定点的序列List，我们应该以List中的每个点为起点，其下一个点Next为终点绘制Bezier曲线。

所以问题变成，如何确定这两个点之间的两个Bezier控制点。

每一小段路径From-To的Bezier曲线并不是独立的，其实收到了其前后两个点的影响（Prev，Next）

我们在绘制每一段路径的时候，引入其前点Prev，和后点Next共同计算当前Bezier曲线的控制点Ctrl1,Ctrl2

如图所示

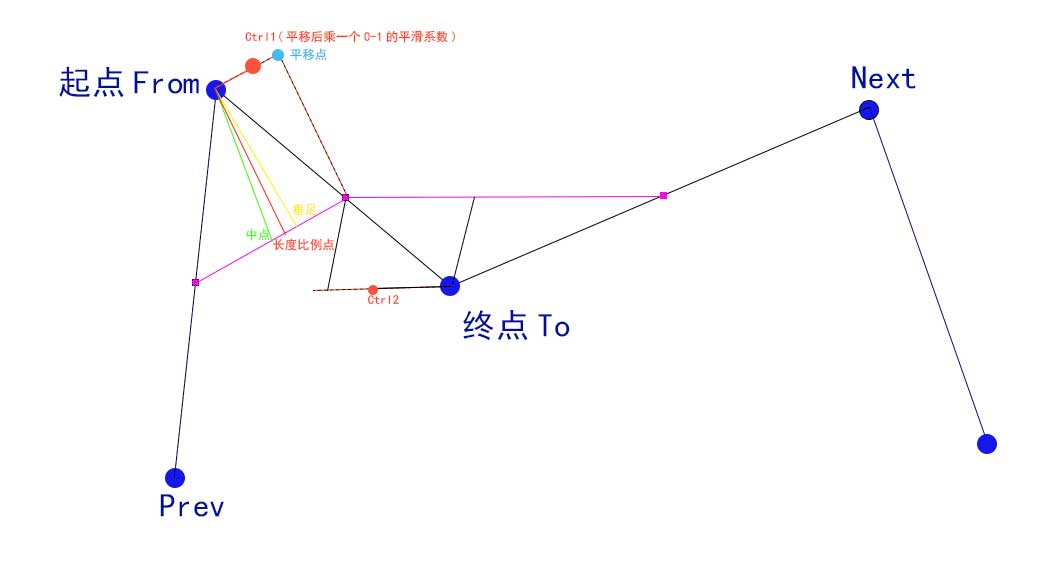
1. 绘制从From到To的Bezier曲线，引入Prev,Next作参考点。
2. 先依次连线4个点，记为线段l1,l2,l3，并求出其中点c1,c2,c3
3. 连接中点，在c1c2上找一点f1, 使 l1:l2 = c1f1:f1c2。也就是 c1f1 = c1c2 * l1/(l1+l2)。我叫它线段比例法。看到有些算法是求其垂足，或者中点，尝试之后发现这个线段比例点绘制的曲线最流畅
4. 将线段 f1c2 平移到 起始点 From上，另一个端点就是所求的控制点Ctrl1。
5. 通常我们会设置一个0-1的平滑度，乘以要平移的线段f1c2，然后得出最终的控制点。如果平滑度为0，那么其控制点就变成From本身，我们所画出来的图形就是折线。
6. 同理求出终点To的控制点Ctrl2，计算过程注意平移位置关系。

我们留意到，当绘制第一段或者最后一段曲线时，没有其前后参考点。这里我的做法是如果该点没有Prev，Prev等于自身；如果没有Next，令Next等于To。仅供参考

简单代码示例

Ps. 这段代码并不能直接运行，仅仅是帮助理解，其中大部分点用向量表示，并省略了向量的实现细节。（如果只是想Ctrl+v的程序员，希望你从来没看过这边文章）

    /**
     * 获取线段AB的k比例点，默认为1/2中点
     * @param {*} a
     * @param {*} b
     * @param {*} k
     */
    getCenterPoint: function(a, b, k=0.5) {
        return a.add(b.sub(a).mul(k)); // 向量加减乘法，下同。a+(b-a)*k => 点a平移ab的k倍距离
    },

    /**
     * 获取以c点为起点，以向量ab的平移的终点
     * @param {*} a
     * @param {*} b
     * @param {*} c
     */
    getTransionPoint: function(a, b, c) {
        return c.add(b.sub(a).mul(this.smooth)); // 平移并乘以平滑度
    },

    /**
     * 计算Bezier控制点
     * @param {*} from
     * @param {*} to
     * @param {*} prev
     * @param {*} next
     */
    getBezierControlPoint: function(from, to, prev, next) {
        let p1 = this.getCenterPoint(prev, from);
        let p2 = this.getCenterPoint(from, to);
        let p3 = this.getCenterPoint(to, next);

        let f1,f2;
        // 使用垂足,不理想
        // f1 = this.getFootPoint(p1, p2, from, f1);
        // f2 = this.getFootPoint(p2, p3, to, f2);

        // 使用中点,不理想
        // f1 = this.getCenterPoint(p1, p2);
        // f2 = this.getCenterPoint(p2, p3);

        // 使用中点距离的比例点
        let len1 = prev.sub(from).mag(); // mag()计算向量prev-from的距离
        let len2 = from.sub(to).mag();
        let len3 = to.sub(next).mag();
        f1 = this.getCenterPoint(p1, p2, len1/(len1+len2)); // p1到p2的k倍距离点
        f2 = this.getCenterPoint(p2, p3, len2/(len2+len3));

        // 基于比例点作平移得到控制点 [Ctrl1, Ctrl2]
        return [this.getTransionPoint(f1, p2, from), this.getTransionPoint(f2, p2, to)];
    },

判断某一点是否在我们的连续Bezier曲线上

换句话说，判断鼠标当前位置是否选中某一段Bezier曲线

1. 如果序列点List的X有序（或者Y有序），（常见的例子是绘制图表，X坐标轴是有序排列的），那么我们先依次对比所有的序列点X坐标，确定其唯一所在区间
2. 否则，我们要对每一小段Bezier曲线进行判断
3. 判断Bezier上的一点，我们需要理解Bezier曲线的原理和其函数。我们把这段曲线看作是一条路径，假设从起点走到终点，需要花费10000个单位时间。对于每个单位之间t，我们可以用函数公式求得其坐标：

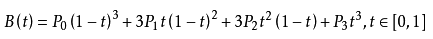
1. 我们拿这10000个坐标点与我们的目标点比较，当其差值在一个可接受的范围内时，我们认为目标点就在我们的Bezier曲线上。
2. 应当注意的是，除了设置的误差范围外，分割的时间片（上面的10000）也会影响到最终结果。如果分割的时间片太少，导致间隙过大使得判断失效。如果分割的时间片太多，又将严重提高计算所消耗的时间。
3. 示例代码

    /**
     * 判断目标点P是否在Bezier曲线(p1,p2,p3,p4)上
     * @param {起点} p1
     * @param {控制点1} p2
     * @param {控制点2} p3
     * @param {终点} p4
     * @param {待判断点} p
     * @param {步长} step
     * @param {误差} range
     * @return Bezier曲线的选中点
     */
    isBezierPoint: function(p1, p2, p3, p4, p, step=0.001, range=0.5) {
        for (let t = 0; t <= 1; t += step) {
            let x = p1.x*Math.pow(1-t, 3) + 3*p2.x*t*Math.pow(1-t, 2) + 3*p3.x*Math.pow(t, 2)*(1-t) + p4.x*Math.pow(t, 3);
            let y = p1.y*Math.pow(1-t, 3) + 3*p2.y*t*Math.pow(1-t, 2) + 3*p3.y*Math.pow(t, 2)*(1-t) + p4.y*Math.pow(t, 3);
            if (Math.abs(x - p.x) < range && Math.abs(y - p.y) < range) {
                return {x,y};
            }
        }
        return null;
    }

Bezier控制点的更新

特别注意一点：

假如我们的序列中某一点的位置发生改变，或者新增了一个序列点，那么其前后将有4个点（忽略端点）的控制点需要重新计算和更新，分别为：

1. 以这个点为From的曲线（自身为起点）
2. 以这个点为To的曲线（上一个点为起点）
3. 以这个点为Prev的曲线（下一个点为起点）
4. 以这个点为Next的曲线（上一个点的上一个点为起点）

for (let i=currentIndex-2, j=0; j<4; i++,j++) {
    // 更新控制点位置
    updateBezierControlPoint(i);
}

以上