LeetCode 周赛 347（2023/05/28）二维空间上的 LIS 最长递增子序列问题

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 提问。

• 往期回顾：LeetCode 单周赛第 346 场 · 仅 68 人 AK 的最短路问题

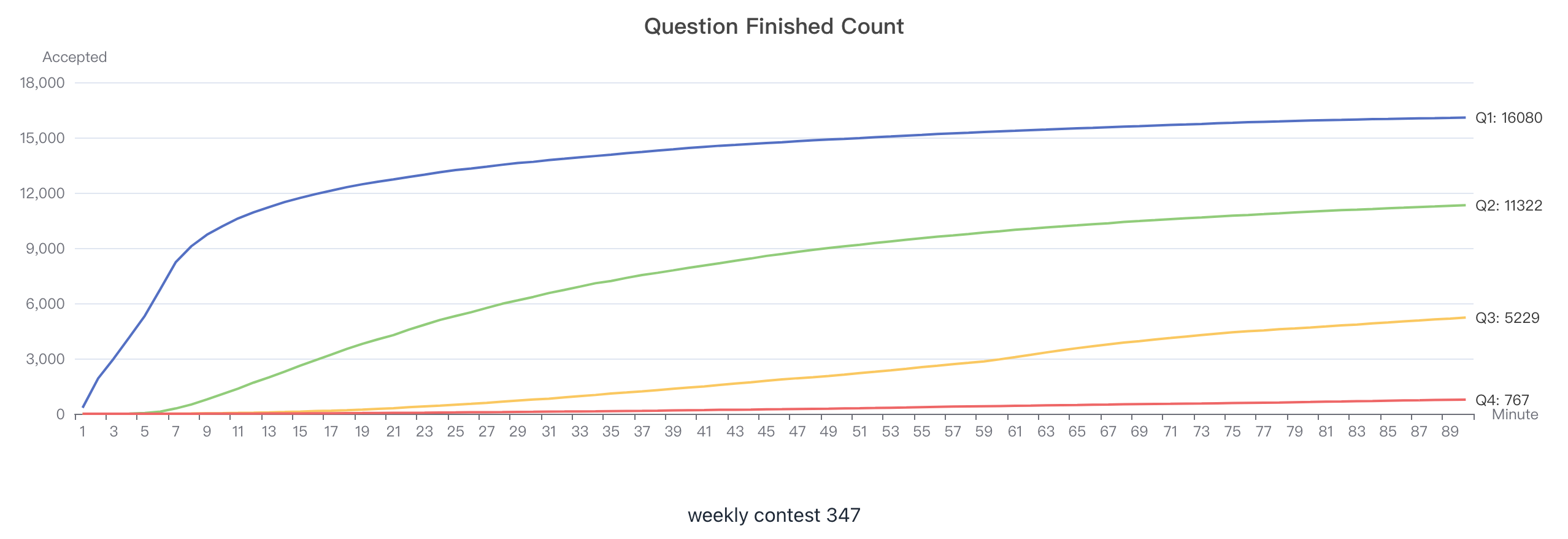
周赛 347 概览

T1. 移除字符串中的尾随零（Easy）

• 标签：模拟、字符串

T2. 对角线上不同值的数量差（Easy）

• 标签：前后缀分解

T3. 使所有字符相等的最小成本（Medium）

• 标签：模拟、贪心

T4. 矩阵中严格递增的单元格数（Hard）

• 标签：排序、动态规划

---

T1. 移除字符串中的尾随零（Easy）

https://leetcode.cn/problems/remove-trailing-zeros-from-a-string/

题解（模拟）

基于 StringBuilder：

class Solution {
    fun removeTrailingZeros(num : String): String {
        if (num.length == 1) return num
        val builder = StringBuilder(num)
        while (builder.last() == '0') {
            builder.deleteCharAt(builder.lastIndex)
        }
        return builder.toString()
    }
}

基于正则表达式匹配：

class Solution {
    fun removeTrailingZeros(num : String): String {
        return num.replace(Regex("0*$"), "")
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$ 不考虑结果字符串

---

T2. 对角线上不同值的数量差（Easy）

https://leetcode.cn/problems/difference-of-number-of-distinct-values-on-diagonals/

题解（前后缀分解）

第一次扫描增加正权，第二次扫描增加负权：

class Solution {
    fun differenceOfDistinctValues(grid: Array<IntArray>): Array<IntArray> {
        // 两次扫描
        val n = grid.size
        val m = grid[0].size
        val ret = Array(n) { IntArray(m) }

        for (row in 0 until n) {
            var i = row
            var j = 0
            val set = HashSet<Int>()
            while (i < n && j < m) {
                ret[i][j] += set.size
                set.add(grid[i][j])
                i++
                j++
            }
        }

        for (col in 1 until m) {
            var i = 0
            var j = col
            val set = HashSet<Int>()
            while (i < n && j < m) {
                ret[i][j] = set.size
                set.add(grid[i][j])
                i++
                j++
            }
        }

        for (row in 0 until n) {
            var i = row
            var j = m - 1
            val set = HashSet<Int>()
            while (i >= 0 && j >= 0) {
                ret[i][j] = Math.abs(ret[i][j] - set.size)
                set.add(grid[i][j])
                i--
                j--
            }
        }

        for (col in 0 until m - 1) {
            var i = n - 1
            var j = col
            val set = HashSet<Int>()
            while (i >= 0 && j >= 0) {
                ret[i][j] = Math.abs(ret[i][j] - set.size)
                set.add(grid[i][j])
                i--
                j--
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(nm)$
• 空间复杂度：$O(nm)$

---

T3. 使所有字符相等的最小成本（Medium）

https://leetcode.cn/problems/minimum-cost-to-make-all-characters-equal/

题解一（模拟）

从中间开始翻转，将不符合目标的字符向两端推，选择反转到 ‘1’ 和 ‘0’ 两个方案的最优解：

class Solution {

    private fun op(s:String, target:Char) :Long {
        val n = s.length
        var ret = 0L
        var flag = true
        for (i in n / 2 - 1 downTo 0) {
            if ((flag && s[i] != target) || (!flag && s[i] == target)) {
                ret += i + 1
                flag = !flag
            }
        }
        flag = true
        for (i in n / 2 until n) {
            if ((flag && s[i] != target) || (!flag && s[i] == target)) {
                ret += n - i
                flag = !flag
            }
        }
        return ret
    }

    fun minimumCost(s: String): Long {
        return Math.min(op(s,'0'), op(s,'1'))
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

题解二（找规律）

当相邻字符串不相等时，必然需要反转。如果接近左边往左边翻转的成本更低，同时，如果接近右边，往右边翻转的成本更低。

class Solution {
    fun minimumCost(s: String): Long {
        val n = s.length
        var ret = 0L
        for (i in 1 until n) {
            if (s[i - 1] != s[i]) {
                ret += Math.min(i, n - i)
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

---

T4. 矩阵中严格递增的单元格数（Hard）

https://leetcode.cn/problems/maximum-strictly-increasing-cells-in-a-matrix/

• 错误思路：

从最大值开始逆向推导，但是最优路径不一定会经过最大值。

• 正确思路：

只有小的数字才能到大的数字，因此我们先将所有数字进行排序，对于每个数字储存其对应的所有位置。此时，每个位置的 LIS 最长序列长度只跟其排序前面的数字中位于同行和同列的数字有关，即前面数字且处于同行同列的最长路径 + 1。

class Solution {
    fun maxIncreasingCells(mat: Array<IntArray>): Int {
        val n = mat.size
        val m = mat[0].size
        var ret = 0
        // 排序
        val map = TreeMap<Int, MutableList<IntArray>>()
        for (i in 0 until n) {
            for (j in 0 until m) {
                map.getOrPut(mat[i][j]) { LinkedList<IntArray>() }.add(intArrayOf(i, j))
            }
        }
        val rowMax = IntArray(n)
        val colMax = IntArray(m)
        // 枚举
        for ((x, indexs) in map) {
            val mx = IntArray(indexs.size)
            // LIS
            for (i in indexs.indices) {
                mx[i] = Math.max(rowMax[indexs[i][0]], colMax[indexs[i][1]]) + 1
                ret = Math.max(ret, mx[i])
            }
            for (i in indexs.indices) {
                rowMax[indexs[i][0]] = Math.max(rowMax[indexs[i][0]], mx[i])
                colMax[indexs[i][1]] = Math.max(colMax[indexs[i][1]], mx[i])
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(nm·lg(nm))$ 瓶颈在排序
• 空间复杂度：$O(nm)$

---

往期回顾

• LeetCode 单周赛第 346 场 · 仅 68 人 AK 的最短路问题
• LeetCode 单周赛第 345 场 · 体验一题多解的算法之美
• LeetCode 双周赛第 104 场 · 流水的动态规划，铁打的结构化思考
• LeetCode 双周赛第 103 场 · 区间求和的树状数组经典应用