Day5网络流

算法

无源汇上下界可行流

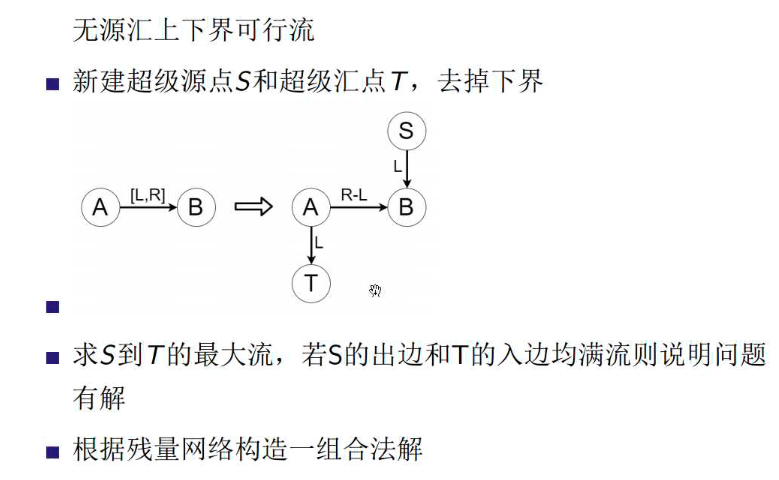
先强制流过l的流量

从s到每个正权点连流量为l的流量

从每个负权点向t连-l的流量

如果容量为0，则不连边

有源汇上下界最大流

去掉下界

先求出可行流

再求S到T的最大流

有源汇上下界最小流

直接应用

poj1149

我的思路

建一个点S，到每个顾客，连INF的边，每个顾客

正解

1.用分层图，建n*m个点

2.直接从S向每个人连边，记录下每个猪圈打开的人的先后顺寻，先来的人向后来的人连边

BZOJ2406

Solution

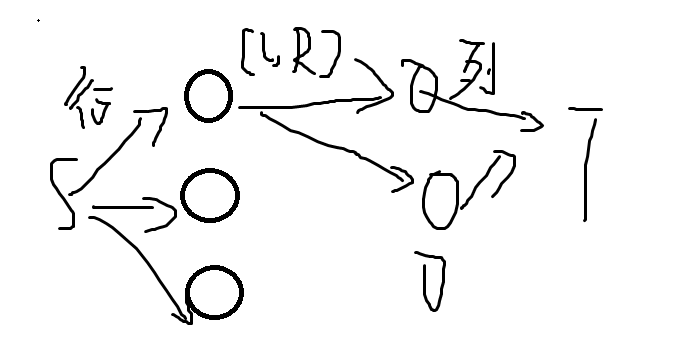
路径覆盖模型

路径覆盖无交集

链覆盖可以有交集

起点，终点的度数都为1

最小化$n-\sum{d}$=最大化$\sum{d}$d为入度

把原图的点都进行拆点

路径覆盖：

若i，j有边，则从i到j'连边

所有边的边权均为1

链覆盖：

用floyd求传递闭包

从一个点向它能到达的点都连边

用最小流解决

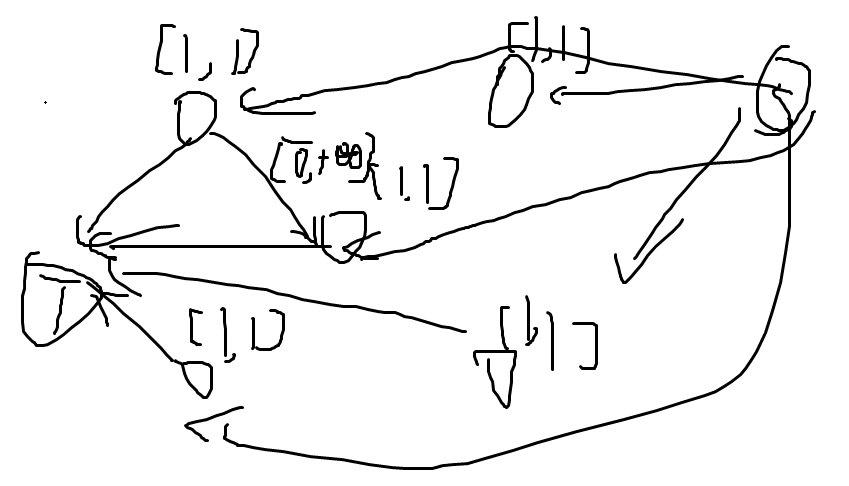
链覆盖把每个点的上限改为INF

魔术球问题

Solution

CTSC2006

最小链覆盖

Dilworth定理

例如<=号

自反性：x<=x

反对称性：x<=y , y<=x —>x==y

传递性：x<=y,y<=z—>x<=z

(<,>不满足偏序关系，不满足第二条性质)

（DAG满足偏序关系，有向图不满足）

反链：两点之间不能相互到达

定理：

TJOI2016XX数学

暴力

拆成n*m个点，每个点的权值下界为给定的权值，上界为INF

优化

对所有点选一条点权和最大的

从左下到右上DP

时间分层

网络流24题星际XXXX

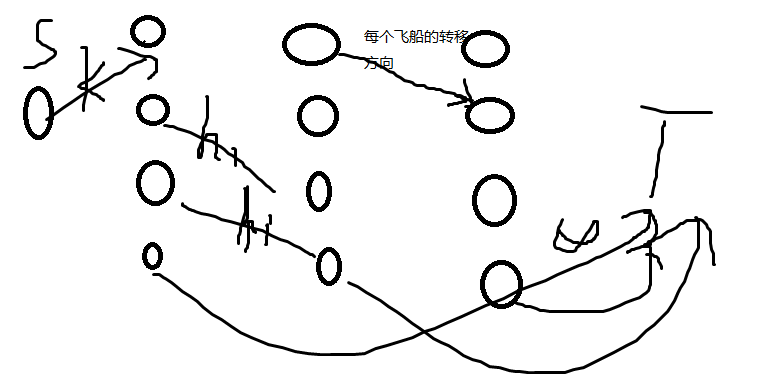
当最大流为k的时候结束

[HNOI2007]紧急疏散

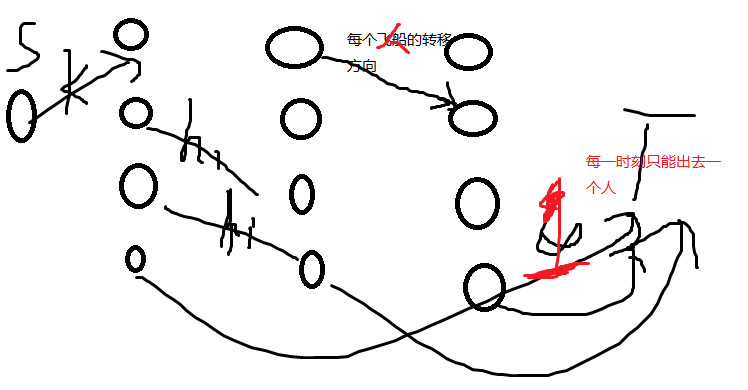
回路限制

POI2010

solution

给每条边定向&&判断是否连通

每条边定向后会使一个点的入度加1，会使一个点的入度减1

先随便定向并保留一次反向机会

可以把每次反向看成一条权值为2的增广路

把点权预先除以二，验证图是否能满流

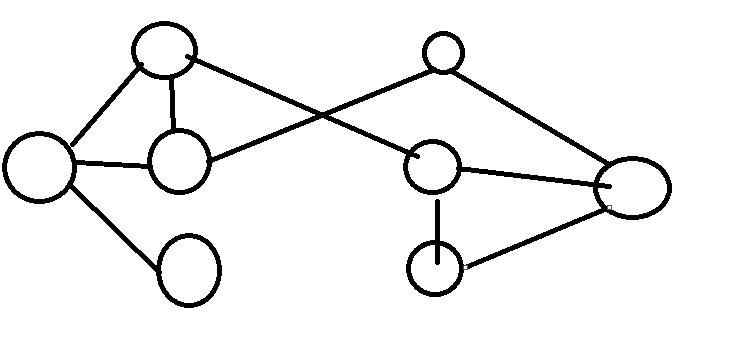
BZOJ4215

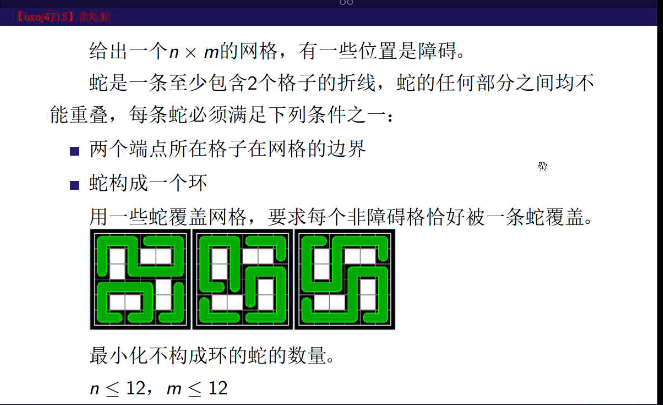
对一个网格进行黑白染色，搞成二分图

用流量为2的边去限制度数为2

如果图满流，那么就存在所有蛇都构成环的方案

找方案的时候看哪些边满流了

如果蛇不构成环，

对于边界上的点，设置其权值为[1,2]，对于非边界上的点，其权值为[2,2]

求最大流

最大权闭合子图

模型

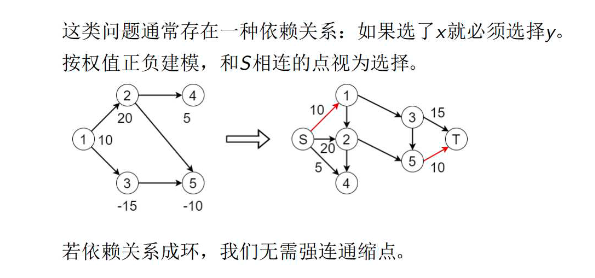
所有与S相连的点视为不选择

所有与T相连的点视为选择

有环的情况可以不缩点，（缩点也可以）

TJOI2015 线性代数

Bij*Ai*Aj

Ci*Ai

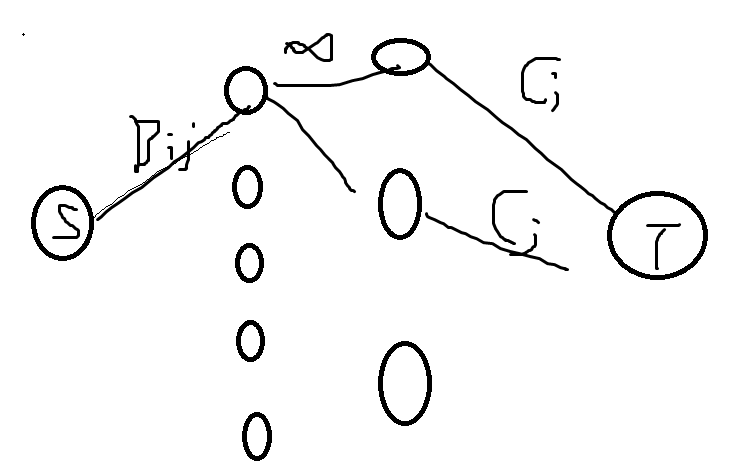
COdefoeceXXX

若不考虑限制条件

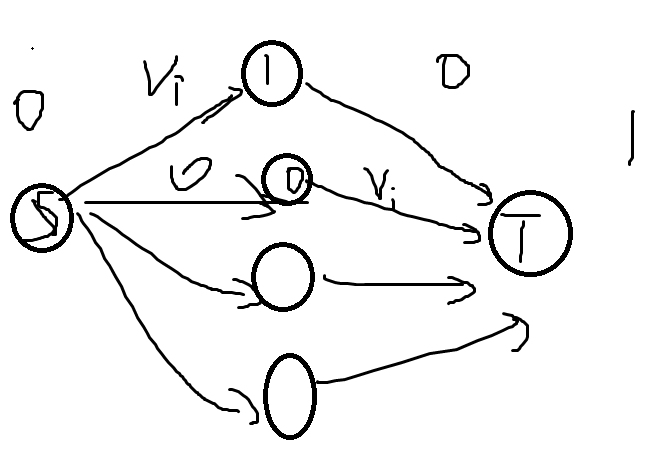
限制条件

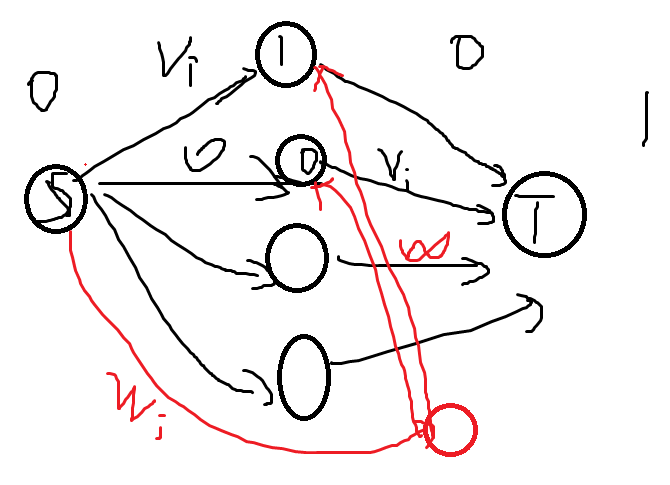
从S向新加的点连Wi边

从新加的点向中间的三个点连INF的边

CEOI?

转化为最小割

BZOJ3774

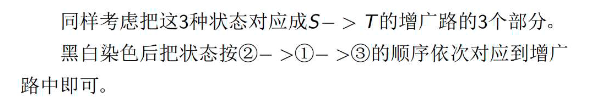
平面图对偶图

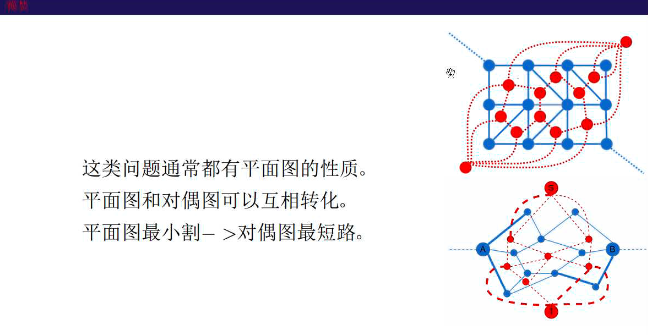
狼抓兔子

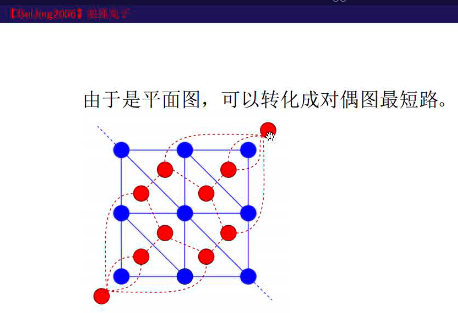
NOI2010海拔

相当于S和T之前求最小割

距离限制

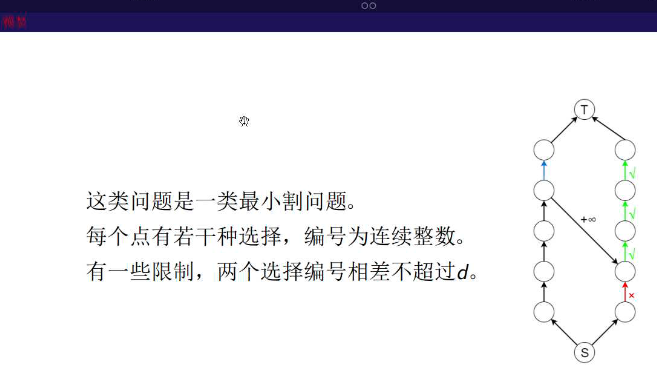
HNOI拍照

变形

CTSC2009

根据曼哈顿距离的性质

分别最优化横纵坐标

Hall定理

k-完备匹配

首先，贪心的找最大匹配然后删去是显然不对的

证明

想要证明k-正则二分图，只需证明k-1是否存在

假设不存在

左侧的m*k条边若分给右侧<m条边，则有一条边的度数不为1

做法

若原图不存在k-正则二分图则无解

POI2009 Lyz

tag

【CERC2016】Bipartite Blanket

solution

证明

时间复杂度

$2^n*n+2^n*log n$