P1140 相似基因 (dp)

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了44种核苷酸，简记作A,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATG和GTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

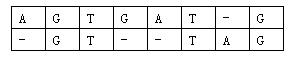
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

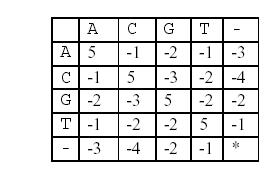
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

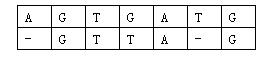
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,T四个字母。1 \le1≤序列的长度\le 100≤100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1：

7 AGTGATG

5 GTTAG

输出样例#1：

14

思路:dp[i][j]表示当前i和j匹配的最优情况 我们知道有三种情况 即i与j直接匹配 i和空格匹配 j和空格匹配 我们选取这三个的最大值

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
#define ll long long int
using namespace std;
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
int moth[]={,,,,,,,,,,,,};
int dir[][]={, ,,};
int dirs[][]={, ,, ,-, ,,-, -,- ,-, ,,- ,,};
const int inf=0x3f3f3f3f;
const ll mod=1e9+;
int c[][]={    {,-,-,-,-},
                {-,,-,-,-},
                {-,-,,-,-},
                {-,-,-,,-},
                {-,-,-,-,}
};
int dp[][]; //i和j匹配的最优解
int main(){
    ios::sync_with_stdio(false);
    int n,m;
    string a,b;
    cin>>n>>a>>m>>b;
    map<char,int> mm;
    mm['A']=;
    mm['C']=;
    mm['G']=;
    mm['T']=;
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++)
            dp[i][j]=-inf;
    dp[][]=;
    for(int i=;i<=n;i++){
        dp[i][]=dp[i-][]+c[mm[a[i-]]][]; //初始化
    }
    for(int i=;i<=m;i++)
        dp[][i]=dp[][i-]+c[][mm[b[i-]]]; //初始化
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++){
            dp[i][j]=max(dp[i][j],dp[i-][j]+c[mm[a[i-]]][]); //i和空格匹配
            dp[i][j]=max(dp[i][j],dp[i][j-]+c[][mm[b[j-]]]); //j和空格匹配
            dp[i][j]=max(dp[i][j],dp[i-][j-]+c[mm[a[i-]]][mm[b[j-]]]); //i和j匹配
        }
    cout<<dp[n][m]<<endl;
    return ;
}