二分图最大权匹配问题&&KM算法讲解 && HDU 2255 奔小康赚大钱

作者：logosG

链接：https://www.cnblogs.com/logosG/p/logos.html （讲解的KM算法，特别厉害！！！）

KM算法：

现在我们来考虑另外一个问题：如果每个员工做每件工作的效率各不相同，我们如何得到一个最优匹配使得整个公司的工作效率最大呢？

这种问题被称为带权二分图的最优匹配问题，可由KM算法解决。

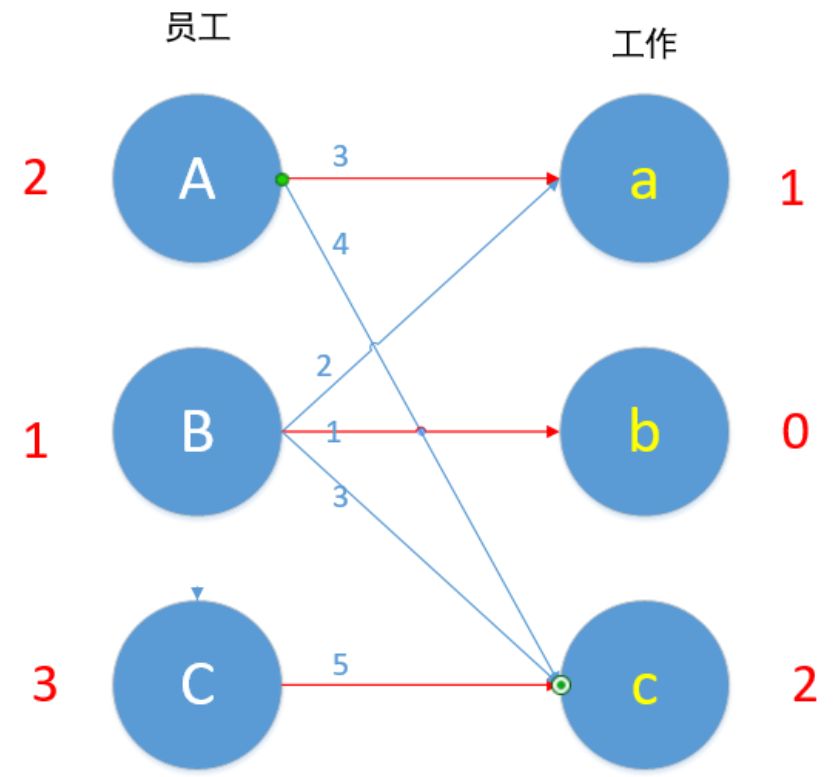
比如上图，A做工作a的效率为3，做工作c的效率为4......以此类推。

不了解KM算法的人如何解决这个问题？我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可。这不失为一个解决方案，但是，如果公司员工的数量越来越多，此种算法的实行难度也就越来越大，我们必须另辟蹊径：KM算法。

KM算法解决此题的步骤如下所示：

1.首先对每个顶点赋值，将左边的顶点赋值为最大权重，右边的顶点赋值为0。

如图，我们将顶点A赋值为其两边中较大的4。

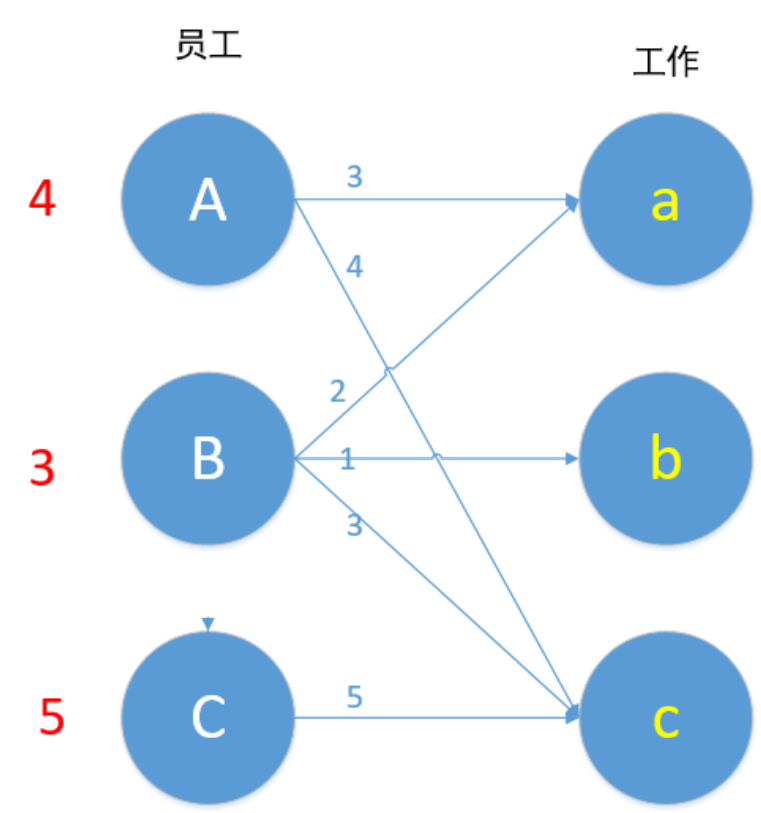
2.进行匹配，我们匹配的原则是：只与权重相同的边匹配，若是找不到边匹配，对此条路径的所有左边顶点-1，右边顶点+1，再进行匹配，若还是匹配不到，重复+1和-1操作。（这里看不懂可以跳过，直接看下面的操作，之后再回头来看这里。）

对A进行匹配，符合匹配条件的边只有Ac边。

匹配成功！

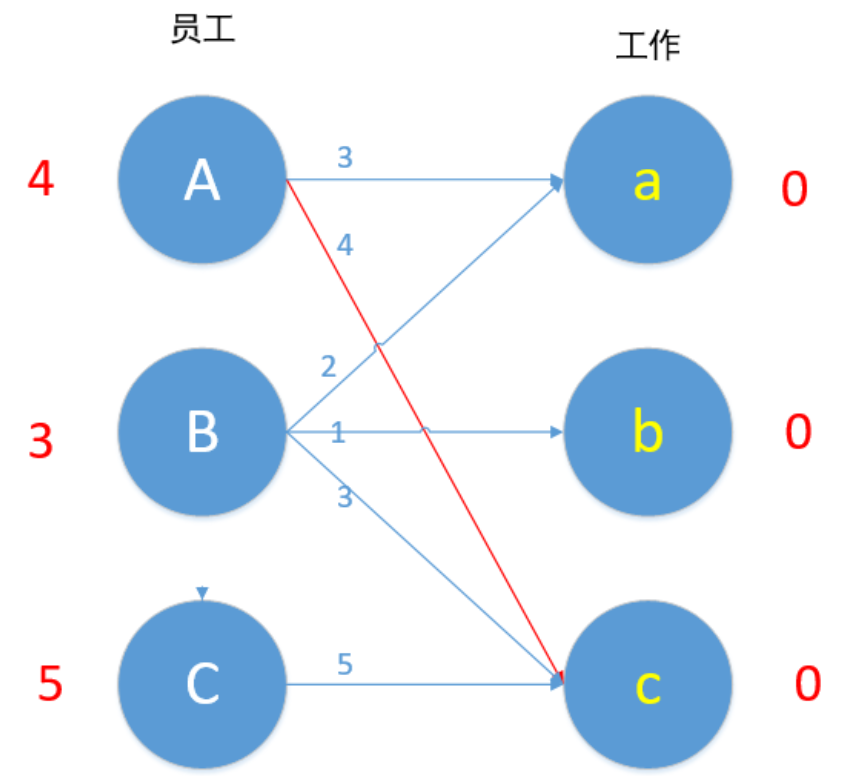
接下来我们对B进行匹配，顶点B值为3，Bc边权重为3，匹配成~ 等等，A已经匹配c了，发生了冲突，怎么办？我们这时候第一时间应该想到的是，让B换个工作，但根据匹配原则，只有Bc边 3+0=0 满足要求，于是B不能换边了，那A能不能换边呢？对A来说，也是只有Ac边满足4+0=4的要求，于是A也不能换边，走投无路了，怎么办？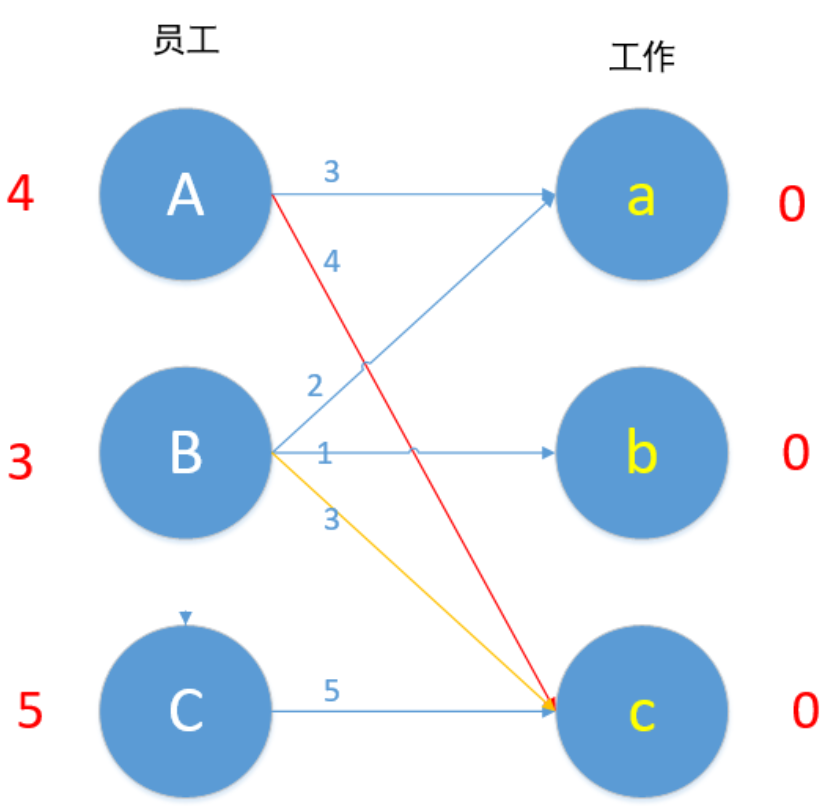

从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个员工找到他们工作效率最高的工作，但是，有些工作会冲突，比如现在，B员工和A员工工作c的效率都是最高，这时我们应该让A或者B换一份工作，但是这时候换工作的话我们只能换到降低总体效率值的工作，也就是说，如果令R=左边顶点所有值相加，若发生了冲突，则最终工作效率一定小于R，但是，我们现在只要求最优匹配，所以，如果A换一份工作降低的工作效率比较少的话，我们是能接受的（对B同样如此）。

在KM算法中如何体现呢？

现在参与到这个冲突的顶点是A,B和c，令所有左边顶点值-1，右边顶点值+1，即 A-1,B-1. c+1，结果如下图所示。

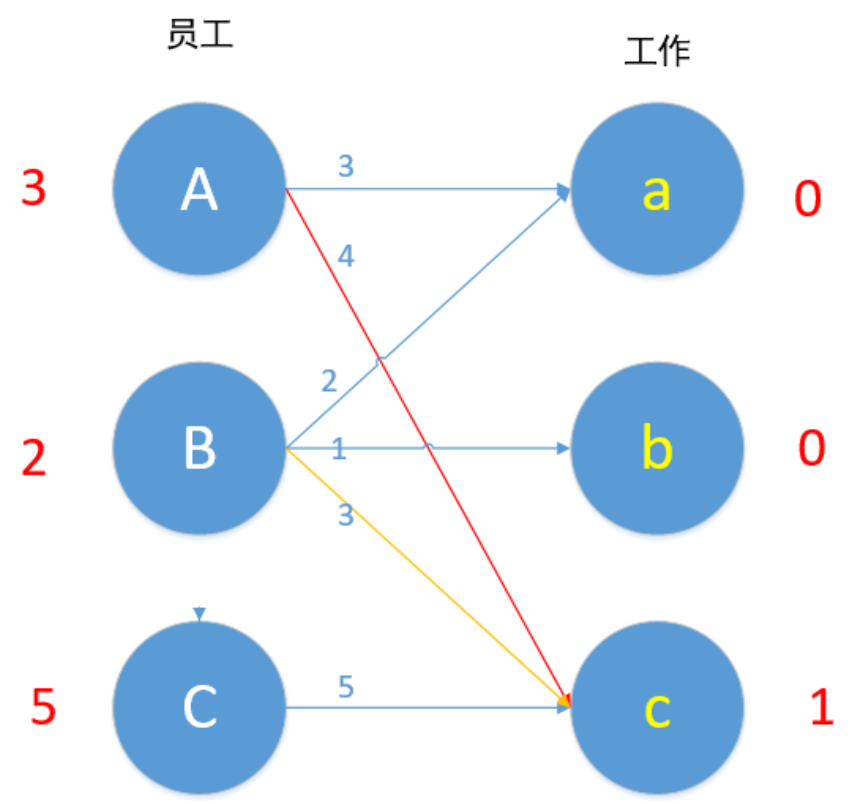
我们进行了上述操作后会发现，若是左边有n个顶点参与运算，则右边就有n-1个顶点参与运算，整体效率值下降了1*（n-（n-1））=1，而对于A来说，Ac本来为可匹配的边，现在仍为可匹配边（3+1=4），对于B来说，Bc本来为可匹配的边，现在仍为可匹配的边（2+1=3），我们通过上述操作，为A增加了一条可匹配的边Aa，为B增加了一条可匹配的边Ba。

现在我们再来匹配，对B来说，Ba边 2+0=2，满足条件，所以B换边，a现在为未匹配状态，Ba匹配！

我们现在匹配最后一条边C，Cc 5+1！=5，C边无边能匹配，所以C-1。

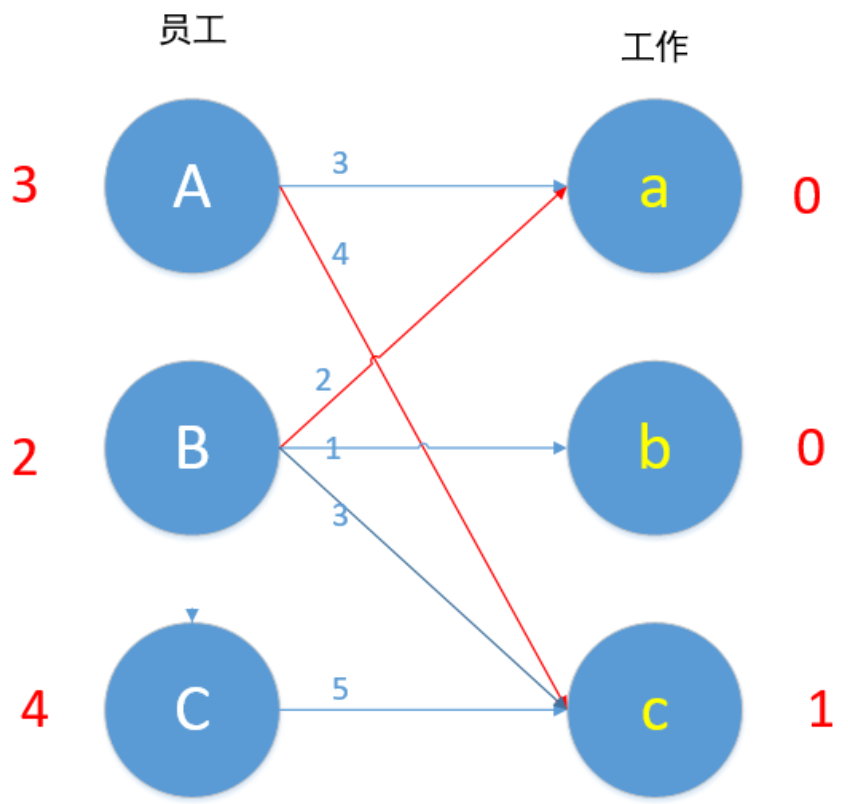
现在Cc边 4+1=5，可以匹配，但是c已匹配了，发生冲突，C此时不能换边，于是便去找A，对于A来说，Aa此时也为可匹配边，但是a已匹配，A又去找B。

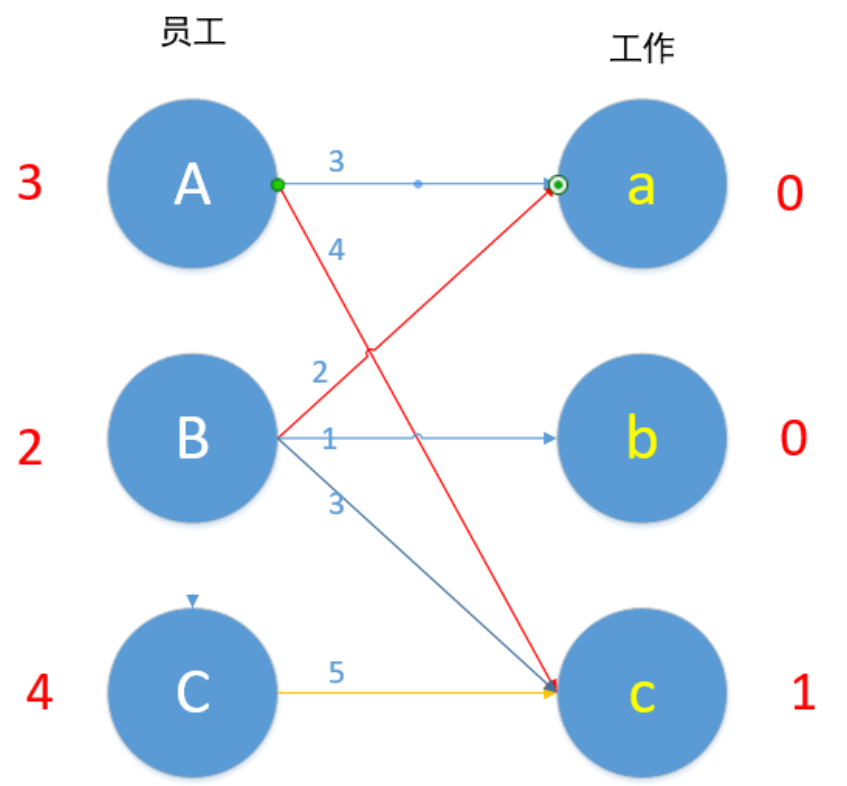
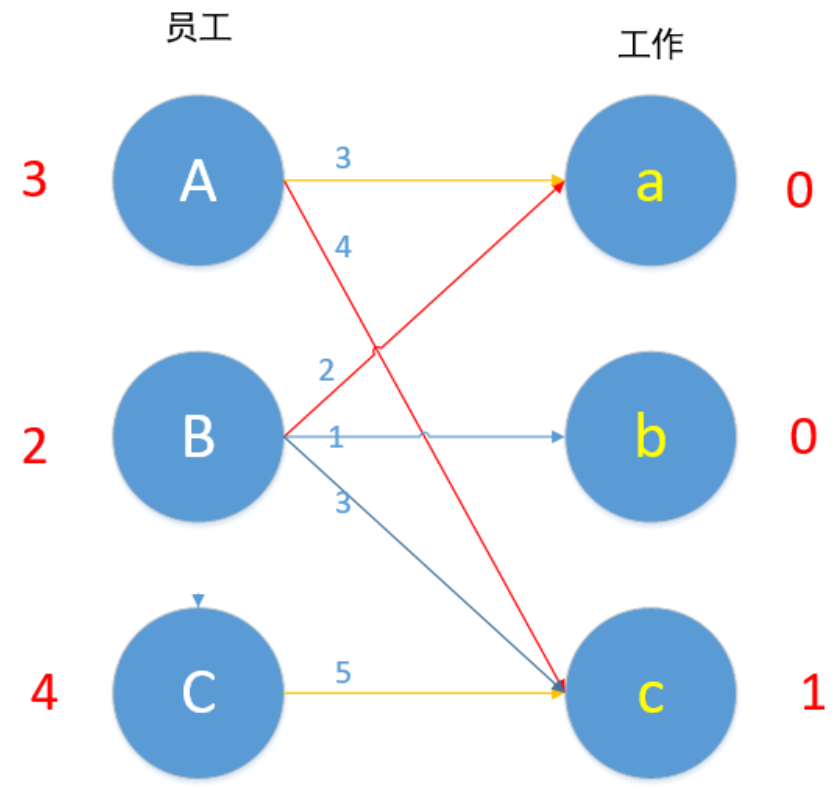
B现在无边可以匹配了，2+0！=1 ，现在的路径是C→c→A→a→B，所以A-1,B-1,C-1,a+1，c+1。如下图所示。

对于B来说，现在Bb 1+0=1 可匹配！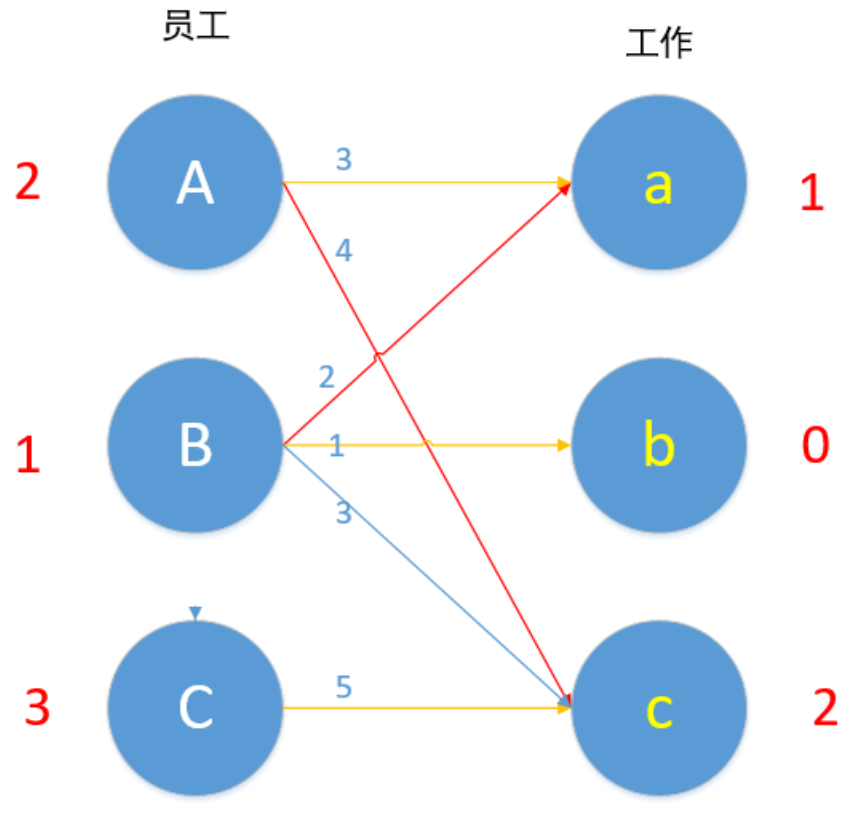

使用匈牙利算法，对此条路径上的边取反。

如图，便完成了此题的最优匹配。

读者可以发现，这题中冲突一共发生了3次，所以我们一共降低了3次效率值，但是我们每次降低的效率值都是最少的，所以我们完成的仍然是最优匹配！

这就是KM算法的整个过程，整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终我们完成的就是最优匹配！

下面便根据HDU 2255 奔小康赚大钱 给出KM代码：

题意：

n间房子，n个人。每一个人对每一间房子有自己的估价，他们会按照自己的估价买房子。现在你需要将每一间房子分给每一个人，这些人会按照自己的估价给你钱。你需要让最后得到的总钱数最大

题解：

很显然就是一道最大权匹配

代码：

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<string.h>
 4 #include<iostream>
 5 #include<queue>
 6 #include<vector>
 7 using namespace std;
 8 const int maxn=510;
 9 const int INF=0x3f3f3f3f;
10 int n;
11 int w[maxn][maxn],link[maxn],matchx[maxn],matchy[maxn];
12 int visitx[maxn],visity[maxn];
13 int sum[maxn];
14 int dfs(int x)
15 {
16     visitx[x]=1;
17     for(int i=1;i<=n;++i)
18     {
19         if(visity[i]) continue;
20         int temp=matchx[x]+matchy[i]-w[x][i];
21         if(!temp)
22         {
23             visity[i]=1;
24             if(link[i]==-1 || dfs(link[i]))
25             {
26                 link[i]=x;
27                 return 1;
28             }
29         }
30         else if(sum[i]>temp)
31             sum[i]=temp;
32     }
33     return 0;
34 }
35 int km()
36 {
37     memset(link,-1,sizeof(link));
38     memset(matchy,0,sizeof(matchy));
39     for(int i=1;i<=n;++i)
40     {
41         matchx[i]=-INF;
42         for(int j=1;j<=n;++j)
43         {
44             if(w[i][j]>matchx[i])
45                 matchx[i]=w[i][j];
46         }
47     }
48     for(int x=1;x<=n;++x)
49     {
50         for(int i=1;i<=n;++i)
51         {
52             sum[i]=INF;
53         }
54         while(1)
55         {
56             memset(visitx,0,sizeof(visitx));
57             memset(visity,0,sizeof(visity));
58             if(dfs(x)) break;
59             int d=INF;
60             for(int i=1;i<=n;++i)
61             {
62                 if(!visity[i]  && d>sum[i])
63                     d=sum[i];
64             }
65             for(int i=1;i<=n;++i)
66             {
67                 if(visitx[i])
68                     matchx[i]-=d;
69             }
70             for(int i=1;i<=n;++i)
71             {
72                 if(visity[i]) matchy[i]+=d;
73                 else sum[i]-=d;
74             }
75         }
76     }
77     int ans=0;
78     for(int i=1;i<=n;++i)
79     {
80         if(link[i]!=-1)
81             ans+=w[link[i]][i];
82     }
83     return ans;
84 }
85 int main()
86 {
87     while(~scanf("%d",&n))
88     {
89         for(int i=1;i<=n;++i)
90         {
91             for(int j=1;j<=n;++j)
92             {
93                 scanf("%d",&w[i][j]);
94             }
95         }
96         printf("%d\n",km());
97     }
98     return 0;
99 }

带注释的代码：

  1 #include <iostream>
  2
  3 #include <cstring>
  4
  5 #include <cstdio>
  6
  7
  8
  9 using namespace std;
 10
 11 const int MAXN = 305;
 12
 13 const int INF = 0x3f3f3f3f;
 14
 15
 16
 17 int love[MAXN][MAXN];   // 记录每个妹子和每个男生的好感度
 18
 19 int ex_girl[MAXN];      // 每个妹子的期望值
 20
 21 int ex_boy[MAXN];       // 每个男生的期望值
 22
 23 bool vis_girl[MAXN];    // 记录每一轮匹配匹配过的女生
 24
 25 bool vis_boy[MAXN];     // 记录每一轮匹配匹配过的男生
 26
 27 int match[MAXN];        // 记录每个男生匹配到的妹子 如果没有则为-1
 28
 29 int slack[MAXN];        // 记录每个汉子如果能被妹子倾心最少还需要多少期望值
 30
 31
 32
 33 int N;
 34
 35
 36
 37
 38
 39 bool dfs(int girl)
 40
 41 {
 42
 43     vis_girl[girl] = true;
 44
 45
 46
 47     for (int boy = 0; boy < N; ++boy) {
 48
 49
 50
 51         if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次
 52
 53
 54
 55         int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];
 56
 57
 58
 59         if (gap == 0) {  // 如果符合要求
 60
 61             vis_boy[boy] = true;
 62
 63             if (match[boy] == -1 || dfs( match[boy] )) {    // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
 64
 65                 match[boy] = girl;
 66
 67                 return true;
 68
 69             }
 70
 71         } else {
 72
 73             slack[boy] = min(slack[boy], gap);  // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸
 74
 75         }
 76
 77     }
 78
 79
 80
 81     return false;
 82
 83 }
 84
 85
 86
 87 int KM()
 88
 89 {
 90
 91     memset(match, -1, sizeof match);    // 初始每个男生都没有匹配的女生
 92
 93     memset(ex_boy, 0, sizeof ex_boy);   // 初始每个男生的期望值为0
 94
 95
 96
 97     // 每个女生的初始期望值是与她相连的男生最大的好感度
 98
 99     for (int i = 0; i < N; ++i) {
100
101         ex_girl[i] = love[i][0];
102
103         for (int j = 1; j < N; ++j) {
104
105             ex_girl[i] = max(ex_girl[i], love[i][j]);
106
107         }
108
109     }
110
111
112
113     // 尝试为每一个女生解决归宿问题
114
115     for (int i = 0; i < N; ++i) {
116
117
118
119         fill(slack, slack + N, INF);    // 因为要取最小值 初始化为无穷大
120
121
122
123         while (1) {
124
125             // 为每个女生解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止
126
127
128
129             // 记录每轮匹配中男生女生是否被尝试匹配过
130
131             memset(vis_girl, false, sizeof vis_girl);
132
133             memset(vis_boy, false, sizeof vis_boy);
134
135
136
137             if (dfs(i)) break;  // 找到归宿 退出
138
139
140
141             // 如果不能找到 就降低期望值
142
143             // 最小可降低的期望值
144
145             int d = INF;
146
147             for (int j = 0; j < N; ++j)
148
149                 if (!vis_boy[j]) d = min(d, slack[j]);
150
151
152
153             for (int j = 0; j < N; ++j) {
154
155                 // 所有访问过的女生降低期望值
156
157                 if (vis_girl[j]) ex_girl[j] -= d;
158
159
160
161                 // 所有访问过的男生增加期望值
162
163                 if (vis_boy[j]) ex_boy[j] += d;
164
165                 // 没有访问过的boy 因为girl们的期望值降低，距离得到女生倾心又进了一步！
166
167                 else slack[j] -= d;
168
169             }
170
171         }
172
173     }
174
175
176
177     // 匹配完成 求出所有配对的好感度的和
178
179     int res = 0;
180
181     for (int i = 0; i < N; ++i)
182
183         res += love[ match[i] ][i];
184
185
186
187     return res;
188
189 }
190
191
192
193 int main()
194
195 {
196
197     while (~scanf("%d", &N)) {
198
199
200
201         for (int i = 0; i < N; ++i)
202
203             for (int j = 0; j < N; ++j)
204
205                 scanf("%d", &love[i][j]);
206
207
208
209         printf("%d\n", KM());
210
211     }
212
213     return 0;
214
215 }