机器学习--PCA算法代码实现(基于Sklearn的PCA代码实现)

一、基于Sklearn的PCA代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA

digits = datasets.load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)

pca = PCA(n_components=2)
pca.fit(X)
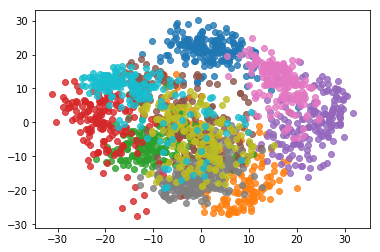
X_reduction = pca.transform(X)

for i in range(10):
    plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)

输出结果：

二、运行过程中出现的问题。

　　初次运行时出现：No module named 'sklearn.model_selection'

　　代码提示指向：

from sklearn.model_selection import train_test_split

　　仔细查看代码，并无问题，问题出在Sklearn的版本过低，Sklearn 0.17.1的版本（及以前）是不包含model_selection库的。

　　运行 Anaconda Prompt（编程使用Anaconda3），输入conda list 可查看各种库的版本，其中scikit-learn的版本显示为：

　　这时就需要更新版本了，可输入：conda update scikit-learn 进行版本更新。

　　若输入：conda update scikit-learn 报错，则可使用：pip install -U scikit-learn 。

　　成功安装之后运行代码，不报错，问题解决。