Reinforcement Learning: An Introduction读书笔记(2)--多臂机

 > 目  录 < 

• k-armed bandit problem
• Incremental Implementation
• Tracking a Nonstationary Problem
• Initial Values
• (*) Upper-Confidence-Bound Action Selection(UCB)
• (*) Gradient Bandit Algorithms
• (*) Associative Search (Contextual Bandits)

 > 笔  记 < 

k-armed bandit problem：

问题定义：重复地从k个options中选择一个，每次都能得到一个reward(每一个option的reward遵循一个稳定的概率)，目标是maximize the total reward。

一个形象的比喻: 医生为若干病人选择治疗方案。

假设我们已经提前知道每个option的expected or mean value，那么每次只需要选择highest value对应的那个action即可；然而一开始我们并不知道该信息or只知道estimated values，那么我们该怎么做呢？我们有两种选择：

choice 1—exploiting--选择greedy action(i.e. 选择具有最大估计值的action)；

choice 2—exploring---may produce the greater total reward in the long run。

为了平衡exploiting和exploring，我们可以采用near-greedy action selection rule 的$ \varepsilon $ -greedy 方法，即大部分情况下(概率为 1- $ \varepsilon $)采取choice 1，少部分情况下(概率为$ \varepsilon $)采用choice 2 。其好处是可以让agent通过探索来提升发现最佳action的可能性。

那么如何估计action values？可以采用sample-average method，即取多次reward的均值，公式如下：

书中给出了一个 10-armed bandit的例子，总共进行2000次选择，下图给出了前1000次的对比：

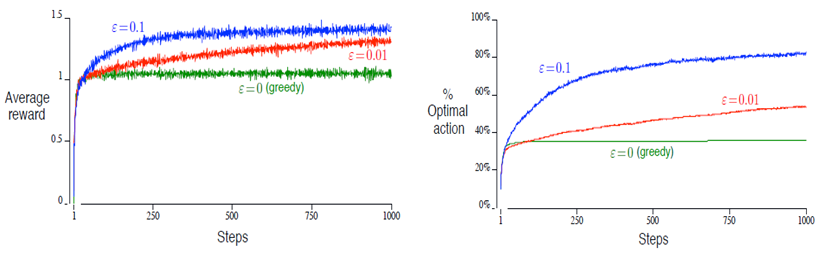
得出结论：(1) greedy method在最开始提升的速度最快，但是后期的表现维持在一个较低的程度；(2) 虽然$ \varepsilon $=0.1比$ \varepsilon $=0.01更早找到optimal action，但最终表现不如$ \varepsilon $=0.01(图中没表现出来，因为还未收敛)。

需要说明的是，$ \varepsilon $-greedy和greedy算法的性能与问题本身密切相关。方差比较大时，前者的优势更明显，但当方差为0时，单纯的greedy算法更好，因为只需要试验一次就可以得到最优action。此外，对于本问题而言，它属于deterministic problem，因为reward和转移函数都是固定的。当问题进一步扩展到nonstationary范畴内，就更需要exploring来适应dynamic。

Incremental Implementation：

如何更有效地计算估计的action values呢？我们一直采用的方法是计算平均值的方式，但弊端是我们需要记录每次的reward (i.e. 下图方法1)，导致占用内存空间。为了解决这一问题，我们将公式变形，发现每次value可以通过递推的方式实现 (i.e. 下图方法2，constant memory & constant per-time-step computation)，这样就不需要多余的空间来存储历史reward了。

可以写成：

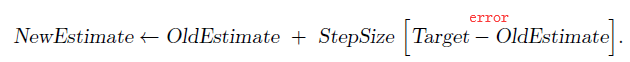
至此，可以给出多臂机的伪代码：

Tracking a Nonstationary Problem：

如果环境变得不再nonstationary (比如多臂机例子中reward probabilities可能会随着时间变化)，那么相对很早以前的rewards，我们通常会给recent rewards一个更大的权值来给出value的估计值 (i.e. Q value)，为此我们引入一个constant step-size parameter $\alpha$，得到

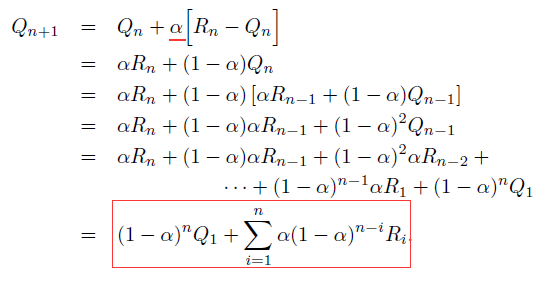
这种方法叫做exponential recency-weighted average。

Initial Values：

设定Initial action values最简单的方法是全部设成0。更好的一种方法是把initial value设置成一个比真实value大的值(比如文中设成5，实际值是一个满足normal 分布(均值=1)的值)，这样all action在开始的时候很快都会被尝试一遍。特别的，如果是stationary problem，我们可以只采用greedy 而不是$ \varepsilon $-greedy method就可以达成目标，但不适用于nonstationary problem，因为没有exploring。

(*) Upper-Confidence-Bound Action Selection(UCB):

$ \varepsilon $-greedy可以让我们实现exploit和explore之间的平衡，但是当我们在explore选择non-greedy action时是随机选取的，有没有更好的方式呢？我们可以在选择的时候重点考虑那些有更大概率是最佳action的集合。

(*) Gradient Bandit Algorithms:

       Gradient Bandit Algorithms通过学习每个action的numerical preference来选择action。preference的数值越大，表明该action被选中的几率越大。不同于基于评估的action values来选择action的方法，这里preference的值与reward并没有直接关系，它只是表达了对不同action的喜好。

下图是上述几种算法在不同参数下的performance对比图：

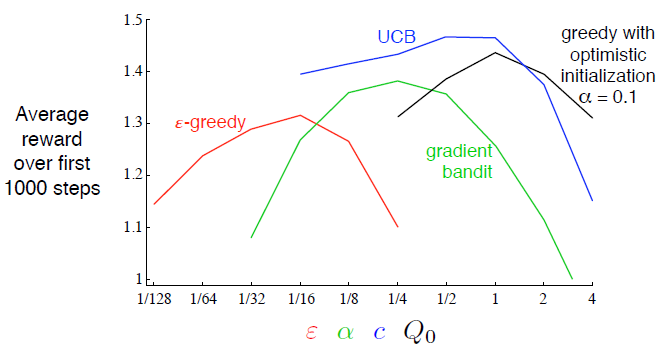
(*) Associative Search (Contextual Bandits)：

之前讨论的赌博机问题是很基本的，不存在states的概念，agent学习到的是在任何情况下的最优行动。实际上，完整的RL问题比多臂机问题更复杂，它包含环境状态，新状态取决于之前的行动，并且回报在时间上也可能存在延迟性。上下文赌博机(Contextual Bandits)比之前讨论的赌博机问题更贴近于RL，因为它引入了state的概念。Contextual Bandits中包含多台赌博机，每台机器的arms的回报概率都不同，state可以告诉我们正在操作哪一台机器。agent的学习目标不再是针对单一机器的最优行动，而是针对多台机器。很多个性化新闻/广告推荐系统都是基于Contextual Bandits的。

拓展阅读(Thompson Sampling，Gittins index)：https://www.sohu.com/a/221811077_775742