retrival and clustering: week 2 knn & LSH 笔记

华盛顿大学 《机器学习》 笔记。

knn

　　k-nearest-neighbors : k近邻法

　　给定一个 数据集，对于查询的实例，在数据集中找到与这个实例最邻近的k个实例，然后再根据k个最邻近点预测查询实例的类别。

　　《统计学习方法》中这样描述的：

　　　　

　　　　

　　K近邻模型是基于训练数据集 对 特征空间的一个划分。

　　　　

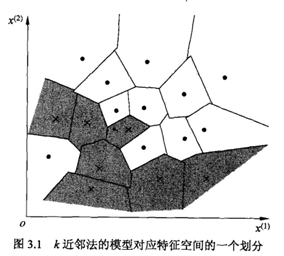
　　当k =1 ，为一种特殊情况，称为最邻近法。

　　Knn算法实现的三个重要问题： 距离度量选择、k值选择，分类决策方法。

　　1. 距离度量选择

　　常用的距离度量有欧式距离、曼哈顿距离等。

　　

　　《统计学习方法》中对距离度量总结：

　　

　　2. K值选择

　　K过小，预测结果对邻近的实例点十分敏感，容易发生过拟合。

　　K过大，估计误差（estimation error）可以减小，但近似误差（approximation error）增大，与实例点隔得很远的训练实例也会对预测起作用。

　　k值一般由交叉验证（cross validation）决定。

　　3.分类决策方法

　　即找到k个最邻近点后，如何得出最后的输出结果。对于分类问题，往往采用多数表决。

　　《统计学习方法》：

　　　　

kd树

　　实现knn算法时，一个主要的问题是如何对数据集快速搜索。其中，暴力搜索复杂度O(Nlogk)，使用特殊的数据结构可以提高搜索效率。

　　Kd树是二叉树，表示对k维空间（k是特征的数量）的一个划分。Kd树是一种存储数据集的方式，以便于进行快速搜索。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构造成一系列的k维超矩形区域，kd树的每个结点对应于一个k维超矩形区域（《统计学习方法》）。

　　

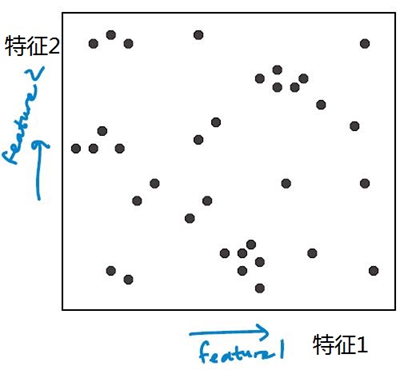
　Kd树的构造方式：以2维空间为例（2个特征）。

　　输入数据集，输出kd树。特征为x = （x[1]， x[2]）

　　开始：根节点为包含整个数据集的矩形区域（如下图所示）。以 feature 1 为切割特征，将整个区域切割成两个子空间，生成两个子节点。

　　

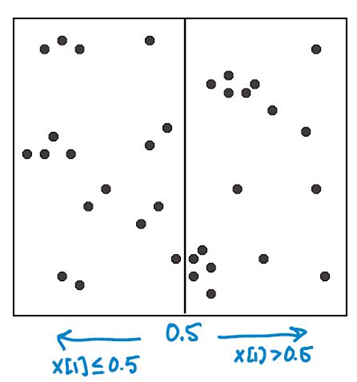
　　　对每个子区域递归，重复切分。直到子区域中包含的数据点少于设定的临界值为止。

　　　　　

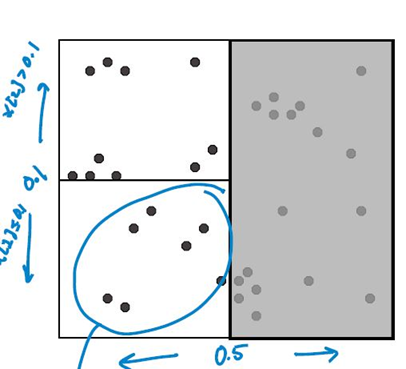
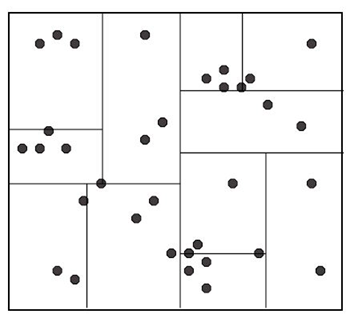
 给定一个查询点，搜素其近邻点的方法：

　　从根节点出发，根据查询点的特征值找到包含查询点的叶子节点，在叶子节点里搜索。

　　　　

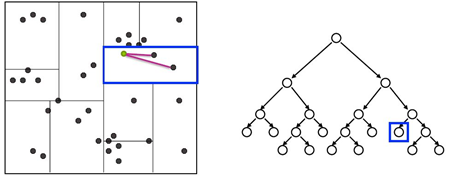
　　之后再回溯到父节点，在父节点的其他子节点中搜索，这样搜索范围被限制在数据集空间的局部区域，提高搜索效率。

　　　　

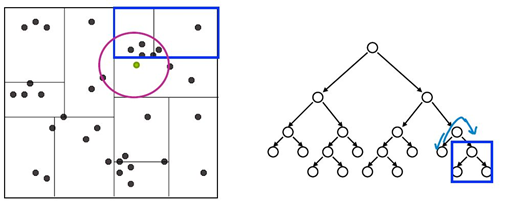
 复杂度：

　　构造二叉树的复杂度：

　　　　  size： 如果每个叶节点只包含1个数据点，一共2N-1个节点。

　　　　depth： O(log N)

　　　　构造时间：O(N log N)

　　查询复杂度：

　　　　找到叶子节点： O ( log N)

　　　　回溯到父节点以及移动到另一个子节点搜素最大花费： O(N)

　　　　复杂度   O ( log N) --> O(N)

　　　(N 为训练集数据点总数)

　　注：通过一些剪枝和优化，查询时间复杂度非常接近O(logN)，kd树适用于低维空间（特征数较少）的情况，维度较高时接近暴力搜索方法。

　　　　对于高维情况，kd树就不是很适用了，可以使用 LSH(locality sensitive hashing )。

LSH

　　LSH(locality sensitive hashing )，LSH通过将数据集的所有数据点随机分区到不同的分箱（bin）来执行有效的邻域搜索。

　　

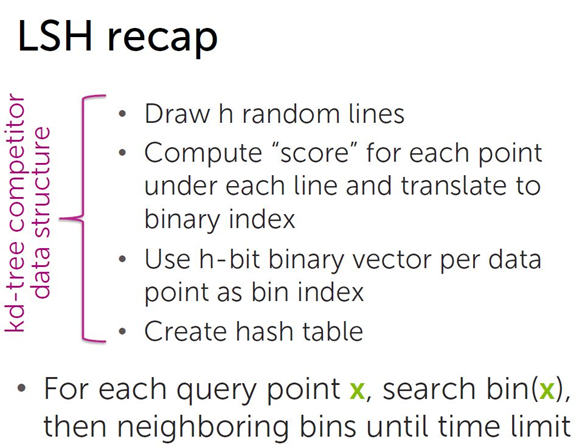
　实现过程：

　　将数据集空间划分成若干个分箱（bin）。

　　　　

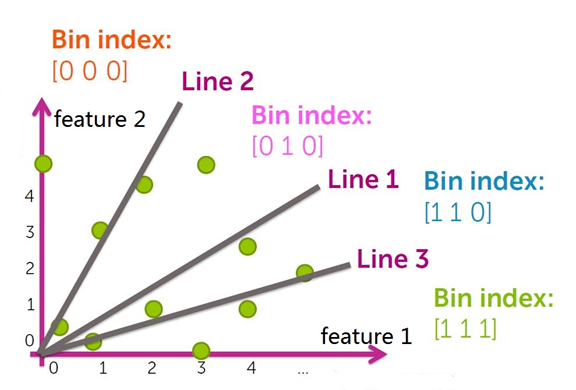
　　根据分箱的划分情况，每个分箱编码（bin index）都可以用一个二进制串表示，即得到所有分箱的hash值。

　　被划分到各个分箱中的数据点用分箱（bin）的 bin index 表示，即相似的数据点（映射到同一个分箱（bin）的数据点）所映射的hash值相同，以此得到数据集中所有点的哈希值，构造哈希表。

　　对于每个查询点 x ，先在相应bin index的分箱中搜索，然后搜索邻近的分箱( bin index相差一位的分箱， 相差两位的分箱 …)。

 　　随机二元投影LSH实现：　

　　模型构建：　

# 输入：
#　　　　data_matrix： 数据集矩阵 ，其中data_matrix[i, j]表示数据点i的特征j的值.
#　　　　k: bin index 位数

# 输出：
#　　　　random_vectors： 用于随机划分数据集的随机向量组
#　　　　index_bits, bin_indices: 分箱编号（bin index），bin_indices[i]:表示数据点i划分到编号为 bin_indices[i]的分箱中
#　　　　lsh_bin: 每个分箱中的数据点，lsh_bin[i]为一个list，表示编号为 i 的分箱中的数据点的序号

def train_lsh_model(data_matrix, k):

    # 第一步：用标准高斯分布生成随机向量组
    # 其中，随机向量的维度 dim 为数据集的大小
    # bin index为 k-bit的二进制串，每个向量可用于计算bin index中的一位，随机向量数量为 k 。
    dim = data_matrix.shape[1]
    num_vector = k
    random_vectors = np.random.randn(dim, num_vector)

    # 第二步：将所有数据点划分到分箱中，并计算分箱编号（bin index）
    index_bits  = data_matrix.dot (random_vectors)  >=  0

    # bin index为k-bit的二进制串，为了方便表示，用对应的整数代替。
    powers_of_two  =  (1 << np.arange(num_vector-1, -1, -1))
    bin_indices  =  index_bits.dot(powers_of_two) 

    # 更新每个分箱中的数据点list
    lsh_bin = {}
    for data_index, bin_index in enumerate(bin_indices):
        if bin_index not in table:
            lsh_bin[bin_index] = []
        lsh_bin[bin_index].append(data_index) #data index为 数据点序号

    model = {'bin_indices': bin_indices,
             'index_bits': index_bits ,
             'lsh_bin': lsh_bin,
             'random_vectors': random_vectors}    

    return model   

　　使用LSH得到搜索邻域：

# 得到待搜索的数据点集

# 输入： 查询数据点x, LSH模型，搜索范围（bin index最多相差几位）
# 输出：  待搜索的数据点集candidate_set

def lsh_search_candidate_set(query_id, lsh_model, search_radius):

    query_bin_bits = lsh_model['index_bits'][query_id]
    lsh_bin =  lsh_model['lsh_bin']
    num_vector = len(query_bin_bits)
    powers_of_two = 1 << np.arange(num_vector-1, -1, -1)

    candidate_set = set()

    for r in xrange(search_radius+1):
        # 罗列所有翻转的位数（combinations：全排列）
        for different_bits in combinations(range(num_vector), r):       

            # 翻转bin index相应的位数，得到邻近分箱的编号
            alternate_bits = copy(query_bin_bits)
            for i in different_bits:
                alternate_bits[i] = (query_bin_bits[i] == False)
            nearby_bin_index = alternate_bits.dot(powers_of_two)

            # 将邻近分箱中的数据点加入 candidate_set
            if nearby_bin in table:
                candidate_set.update(tuple(lsh_bin[nearby_bin]))

    return candidate_set