g2o优化库实现曲线拟合

g2o优化库实现曲线拟合

最近学习了一下g2o优化库的基本使用，尝试着自己写了一个曲线拟合的函数，也就是下面这个多项式函数：

\[y = ax^3 + bx^2 + cx + d
\]

我们以 \(a = 3, b = -2, c=5, b=7\)为例，拟合出的图像大概长这样。

下面简单记录一下思路：

目标函数：

\[\min _{a, b, c,d} \frac{1}{2} \sum_{i=1}^N\left\|y_i-(ax_i^3 + bx_i^2 + cx_i + d))\right\|^2 .
\]

目标就是求解出一组 \(a,b,c,d\)使得观测值和估计值的误差最小化。

• 高斯牛顿法

  推导出每个误差项关于优化变量的导数：

  \[\begin{aligned}
  & \frac{\partial e_i}{\partial a}=-x_i^3\\
  & \frac{\partial e_i}{\partial b}=-x_i^2 \\
  & \frac{\partial e_i}{\partial c}=-x_i \\
  & \frac{\partial e_i}{\partial d}=-1
  \end{aligned}
  \]

  于是 \(\boldsymbol{J}_i=\left[\frac{\partial e_i}{\partial a}, \frac{\partial e_i}{\partial b}, \frac{\partial e_i}{\partial c} \frac{\partial e_i}{\partial d}, \right]^{\mathrm{T}}\), 高斯牛顿法的增量方程为：

  \[\left(\sum_{i=1}^{N} \boldsymbol{J}_i\left(\sigma^2\right)^{-1} \boldsymbol{J}_i^{\mathrm{T}}\right) \Delta \boldsymbol{x}_k=\sum_{i=1}^{N}-\boldsymbol{J}_i\left(\sigma^2\right)^{-1} e_i,
  \]

  代码在附录里，假设要估计的 \(a=3, b=-2,c=5,d=7\)，大概只需要三次迭代就能得到估计的结果。
  
  

• g2o

  优化变量构成一个顶点，每个误差项构成一条边。

  顶点类需要重写变量的重置，更新函数；

  边类需要设置关联的顶点，重写误差计算函数，必要时也可以给出解析导数。

​ 下面我们主要测试一下是否给出误差项关于优化变量的解析导数对g2o求解次数的影响（对应的就是g2o_curve.cpp中雅各比矩阵是否注释）

不提供解析导数	提供解析导数
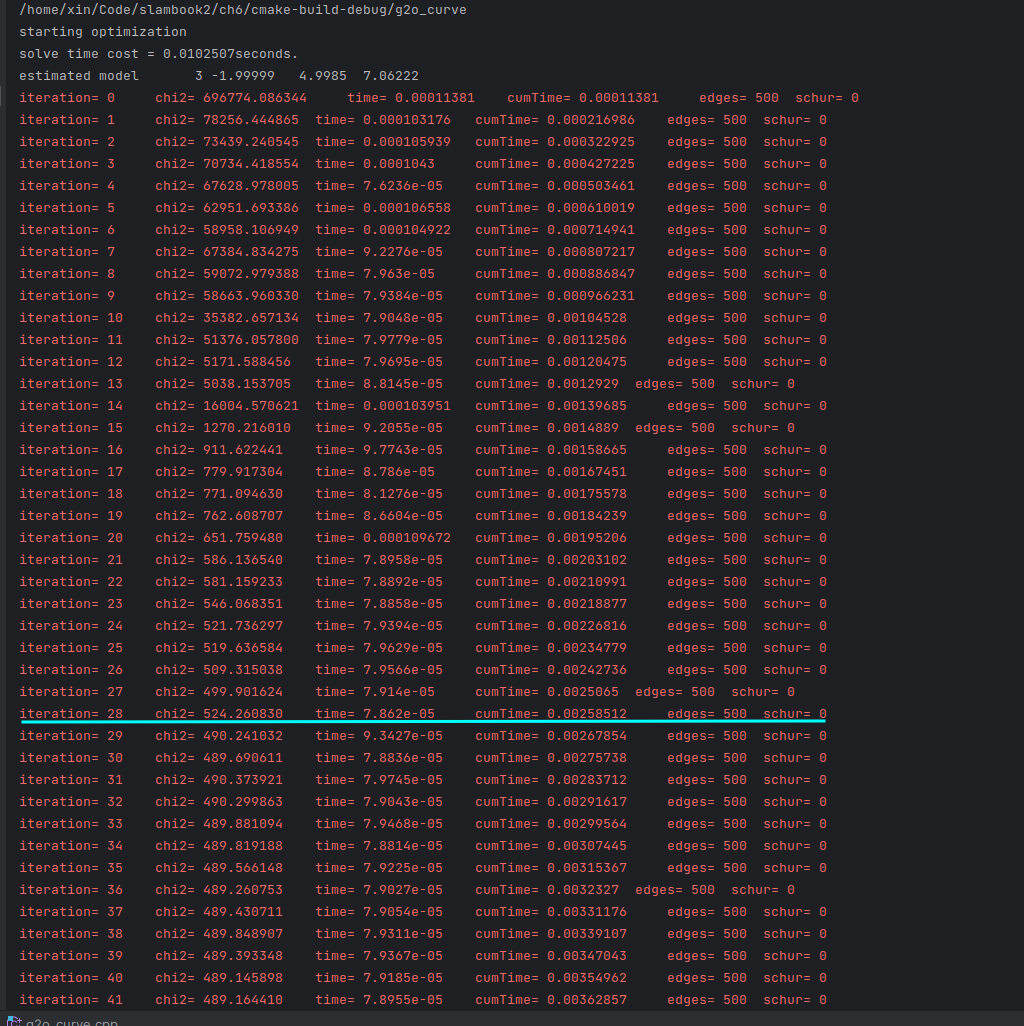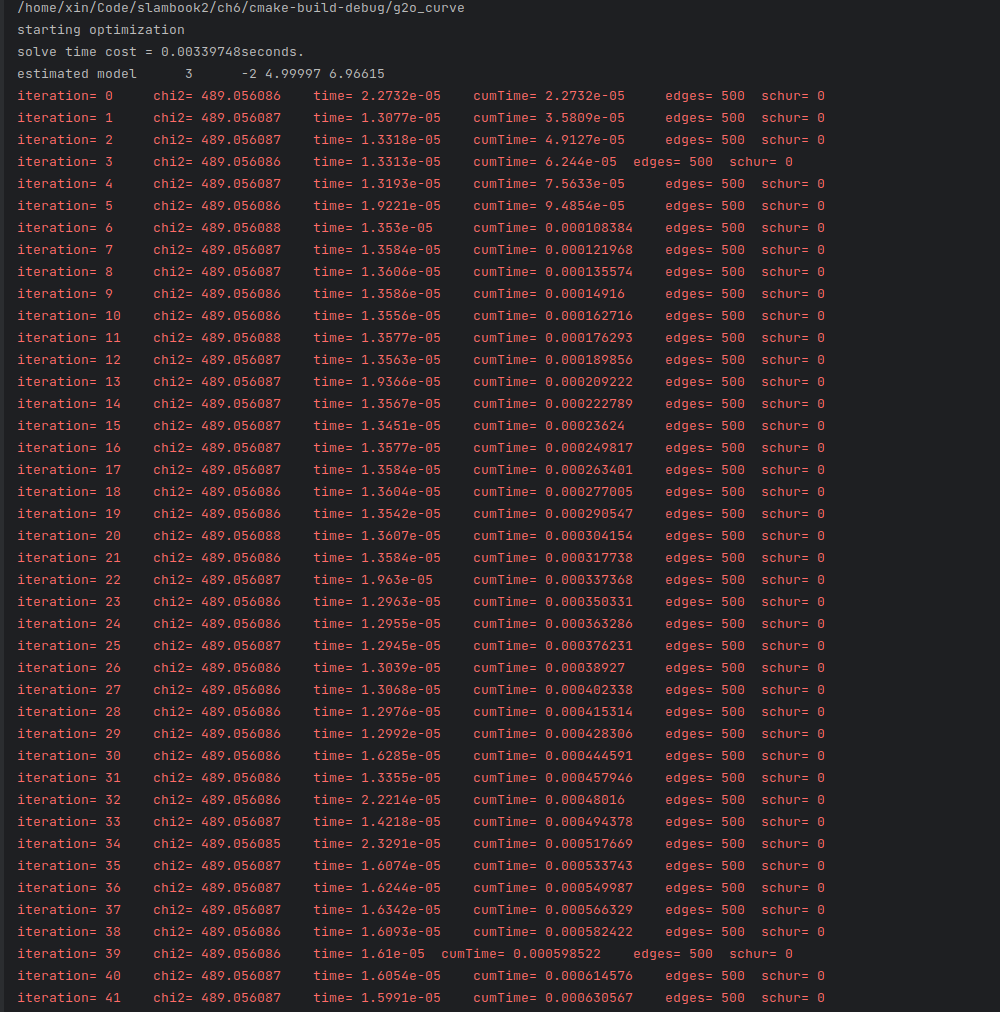0.01s	0.003s

我们可以看到速度差别还挺大的。

附录

gaussNewton.cpp

//
// Created by xin on 23-6-6.
// use g2o curve fitting y = a*x_3 + b*x_2 + c*x + d
//
#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>

using namespace std;

int main() {

    double a = 3.0, b = -2.0, c = 5.0, d = 7; // 真实参数值
    double ae = 1, be = 1, ce = 1, de = 100;  // 初始参数值

    int N = 500; //数据点个数
    double w_sigma = 1.0;
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;

    vector<double> x_data, y_data;
    for (int i = 0; i < N; i++) {
        double x = double(i);
        x_data.push_back(x);
        y_data.push_back(a * pow(x, 3) + b * pow(x, 2) + c*x + d + rng.gaussian(w_sigma * w_sigma));
       //std::cout << x << "," << a * pow(x, 3) + b * pow(x, 2) + c * x + d + rng.gaussian(w_sigma * w_sigma) << endl;
    }

    // 开始Gauss-Newton迭代
    int iterations = 1000;    // 迭代次数
    double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    for (int iter = 0; iter < iterations; iter++) {

        Eigen::Matrix4d H = Eigen::Matrix4d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
        Eigen::Vector4d b = Eigen::Vector4d::Zero();             // bias
        cost = 0;

        for (int i = 0; i < N; i++) { //求每一个数据点的 J 矩阵
            double xi = x_data[i], yi = y_data[i];  // 第i个数据点
            double error = yi - (ae*pow(xi, 3) + be*pow(xi, 2) + ce*xi + de);
            Eigen::Vector4d J; // 雅可比矩阵
            J[0] = -pow(xi, 3);
            J[1] = -pow(xi, 2);
            J[2] = -xi;
            J[3] = -1;

            H += inv_sigma * inv_sigma * J * J.transpose();
            b += -inv_sigma * inv_sigma * error * J;

            cost += error * error;
        }

        // 求解线性方程 Hx=b
        Eigen::Vector4d dx = H.ldlt().solve(b);
        if (isnan(dx[0])) {
            cout << "result is nan!" << endl;
            break;
        }

        if (iter > 0 && cost >= lastCost) {
            cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
            break;
        }

        ae += dx[0];
        be += dx[1];
        ce += dx[2];
        de += dx[3];

        lastCost = cost;

        cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
             "\t\testimated params: " << ae << "," << be << "," << ce << "," << de << endl;
    }

    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

    cout << "estimated abcd = " << ae << ", " << be << ", " << ce  << "," << de << endl;
    return 0;

    return 0;

}

g2o_curve.cpp

//
// Created by xin on 23-6-6.
// use g2o curve fitting y = a*x_3 + b*x_2 + c*x + d
//
#include <iostream>
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <Eigen/Core>
#include <opencv2/core/core.hpp>
#include <cmath>
#include <chrono>

using namespace std;

/// 自定义图优化的顶点 以及 边
class CurveFittingVertex : public g2o::BaseVertex<4, Eigen::Vector4d> {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    // 重置
    virtual void setToOriginImpl() override {
        _estimate << 0, 0, 0, 0;
    }

    // 更新
    virtual void oplusImpl(const double *update) override {
        _estimate += Eigen::Vector4d(update);
    }

    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}
};

class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> { // 误差项的维度， 类型， 关联的顶点
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}

    // 误差函数
    virtual void computeError() override {
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]); //此处拿到关联的顶点
        Eigen::Vector4d abcd = v->estimate();
        _error(0, 0) =
                _measurement - (abcd[0] * pow(_x, 3) + abcd[1] * pow(_x, 2) + abcd[2] * _x + abcd[3]);
    }

    // 雅各比矩阵，可以注释掉对比一下求解速度
    virtual void linearizeOplus() override {
        _jacobianOplusXi[0] = -_x * _x * _x;
        _jacobianOplusXi[1] = -_x * _x;
        _jacobianOplusXi[2] = -_x;
        _jacobianOplusXi[3] = -1;
    }

    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}

public:
    double _x; // 这个误差项对应的自变量x
};

int main() {

    double a = 3.0, b = -2.0, c = 5.0, d = 7; // 真实参数值
    double ae = 1, be = 1, ce = 1, de = 100;  // 初始参数值

    int N = 500; //数据点个数
    double w_sigma = 1.0;
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;

    vector<double> x_data, y_data;
    for (int i = 0; i < N; i++) {
        double x = double(i);
        x_data.push_back(x);
        y_data.push_back(a * pow(x, 3) + b * pow(x, 2) + c*x + d + rng.gaussian(w_sigma * w_sigma));

       std::cout << x << "," << a * pow(x, 3) + b * pow(x, 2) + c * x + d + rng.gaussian(w_sigma * w_sigma) << endl;
    }

    // 构建图优化
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<4, 1>> BlockSolverType;
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型 dense CSparse

    //梯度下降方法
    auto solver = new g2o::OptimizationAlgorithmGaussNewton(
            g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>())
    );
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm(solver);
    optimizer.setVerbose(true);

    //往图中加入顶点
    CurveFittingVertex *v = new CurveFittingVertex();
    v->setId(0);
    v->setEstimate(Eigen::Vector4d(ae, be, ce, de));
    optimizer.addVertex(v);

    //往图中加入边（误差项）
    for(int i = 0; i < N; i++){
        CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
        edge->setId(i);
        edge->setVertex(0, v);
        edge->setMeasurement(y_data[i]);
        edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
        optimizer.addEdge(edge);
    }

    cout << "starting optimization" << endl;
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.initializeOptimization();
    optimizer.optimize(100);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "solve time cost = " << time_used.count() << "seconds." << endl;

    // output 结果
    Eigen::Vector4d abcd_estimate = v->estimate();
    cout << "estimated model" << abcd_estimate.transpose() << endl;
    return 0;

}