机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述
概述
1 从什么叫“维度”说开来
我们不断提到一些语言,比如说:随机森林是通过随机抽取特征来建树,以避免高维计算;再比如说,sklearn中导入特征矩阵,必须是至少二维;上周我们讲解特征工程,还特地提到了,特征选择的目的是通过降维来降低算法的计算成本……这些语言都很正常地被我用来使用,直到有一天,一个小伙伴问了我,”维度“到底是什么?
对于数组和Series来说,维度就是功能shape返回的结果,shape中返回了几个数字,就是几维。索引以外的数据,不分行列的叫一维(此时shape返回唯一的维度上的数据个数),有行列之分叫二维(shape返回行x列),也称为表。
一张表最多二维,复数的表构成了更高的维度。当一个数组中存在2张3行4列的表时,shape返回的是(更高维,行,列)。当数组中存在2组2张3行4列的表时,数据就是4维,shape返回(2,2,3,4)。

数组中的每一张表,都可以是一个特征矩阵或一个DataFrame,这些结构永远只有一张表,所以一定有行列,其中行是样本,列是特征。
针对每一张表,维度指的是样本的数量或特征的数量,一般无特别说明,指的都是特征的数量。除了索引之外,一个特征是一维,两个特征是二维,n个特征是n维。
对图像来说,维度就是图像中特征向量的数量。
特征向量可以理解为是坐标轴,一个特征向量定义一条直线,是一维,两个相互垂直的特征向量定义一个平面,即一个直角坐标系,就是二维,三个相互垂直的特征向量定义一个空
间,即一个立体直角坐标系,就是三维。三个以上的特征向量相互垂直,定义人眼无法看见,也无法想象的高维空间。
降维算法中的”降维“,指的是降低特征矩阵中特征的数量。
上周的课中我们说过,降维的目的是为了让算法运算更快,效果更好,但其实还有另一种需求:数据可视化。从上面的图我们其实可以看得出,图像和特征矩阵的维度是可以相互对应的,即一个特征对应一个特征向量,对应一条坐标轴。所以,三维及以下的特征矩阵,是可以被可视化的,这可以帮助我们很快地理解数据的分布,而三维以上特征矩阵的则不能被可视化,数据的性质也就比较难理解。
2 sklearn中的降维算法
sklearn中降维算法都被包括在模块decomposition中,这个模块本质是一个矩阵分解模块。在过去的十年中,如果要讨论算法进步的先锋,矩阵分解可以说是独树一帜。
矩阵分解可以用在降维,深度学习,聚类分析,数据预处理,低纬度特征学习,推荐系统,大数据分析等领域。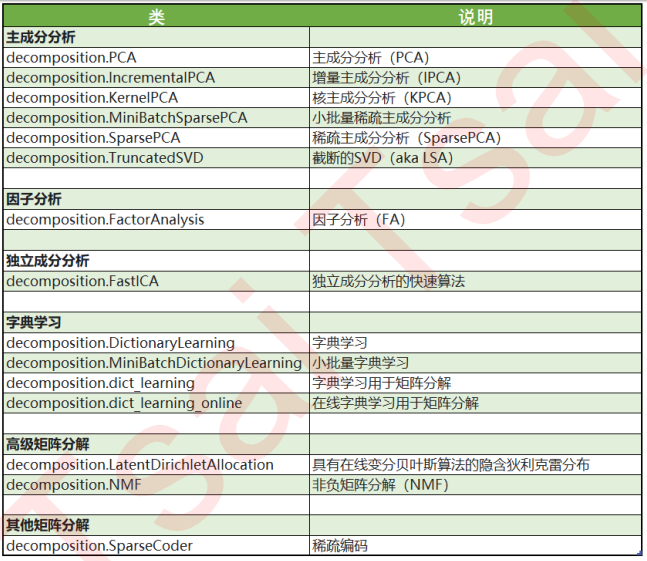
机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述的更多相关文章
- 机器学习实战基础(二十四):sklearn中的降维算法PCA和SVD(五) PCA与SVD 之 重要接口inverse_transform
重要接口inverse_transform 在上周的特征工程课中,我们学到了神奇的接口inverse_transform,可以将我们归一化,标准化,甚至做过哑变量的特征矩阵还原回原始数据中的特征矩阵 ...
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- 机器学习实战基础(二十一):sklearn中的降维算法PCA和SVD(二) PCA与SVD 之 降维究竟是怎样实现
简述 在降维过程中,我们会减少特征的数量,这意味着删除数据,数据量变少则表示模型可以获取的信息会变少,模型的表现可能会因此受影响.同时,在高维数据中,必然有一些特征是不带有有效的信息的(比如噪音),或 ...
- 机器学习实战基础(二十二):sklearn中的降维算法PCA和SVD(三) PCA与SVD 之 重要参数n_components
重要参数n_components n_components是我们降维后需要的维度,即降维后需要保留的特征数量,降维流程中第二步里需要确认的k值,一般输入[0, min(X.shape)]范围中的整数. ...
- 机器学习实战基础(二十五):sklearn中的降维算法PCA和SVD(六) 重要接口,参数和属性总结
到现在,我们已经完成了对PCA的讲解.我们讲解了重要参数参数n_components,svd_solver,random_state,讲解了三个重要属性:components_, explained_ ...
- 机器学习实战基础(二十六):sklearn中的降维算法PCA和SVD(七) 附录
- 机器学习实战基础(二十七):sklearn中的降维算法PCA和SVD(八)PCA对手写数字数据集的降维
PCA对手写数字数据集的降维 1. 导入需要的模块和库 from sklearn.decomposition import PCA from sklearn.ensemble import Rando ...
- 机器学习实战基础(十四):sklearn中的数据预处理和特征工程(七)特征选择 之 Filter过滤法(一) 方差过滤
Filter过滤法 过滤方法通常用作预处理步骤,特征选择完全独立于任何机器学习算法.它是根据各种统计检验中的分数以及相关性的各项指标来选择特征 1 方差过滤 1.1 VarianceThreshold ...
- 机器学习实战基础(十):sklearn中的数据预处理和特征工程(三) 数据预处理 Preprocessing & Impute 之 缺失值
缺失值 机器学习和数据挖掘中所使用的数据,永远不可能是完美的.很多特征,对于分析和建模来说意义非凡,但对于实际收集数据的人却不是如此,因此数据挖掘之中,常常会有重要的字段缺失值很多,但又不能舍弃字段的 ...
随机推荐
- kali设置NAT模式,无法正常上网请试试这个办法
1.释放网卡: dhclient -r eth0 2.自动获取网络 dhclient -v eth0 3.开启22端口 lsof -i :22 4.打开ssh service ssh start sy ...
- dbca oracle 12 c 遇到ora27125
网上大部分方法是把dba组放在内核的,没有效果,可以尝试 google找到一位大神的方案,成功解决 https://oracle-admin.com/2014/01/22/ora-27125-unab ...
- Linux下自己和自己用各种方法进行文件的上传下载
环境: Ubuntu 16.04 1.SCP # 上传 scp /home/sea/Desktop/test.sh sea@192.168.1.31:/home/sea/Desktop/test.sh ...
- Android笔记布局资源文件
在项目的res--layout目录下的文件叫布局资源文件,用于控制页面的布局显示 在Java代码中引用布局资源我们已经很熟悉了. setContentView(R.layout.activity_ma ...
- rust 宏
macro_rules! four { () => {1 + 3}; } fn main(){ println!("{}", 1+four!()); println!(&qu ...
- cb07a_c++_迭代器和迭代器的范围
cb07a_c++_迭代器和迭代器的范围c++primer第4版https://www.cnblogs.com/txwtech/p/12309989.html--每一种容器都有自己的迭代器--所有的迭 ...
- cb06a_c++_顺序容器的定义
/*cb06a_c++_顺序容器的定义顺序容器:vector,数组,尾端操作数据,快速随机访问list 链表,快速插入数据deque数组,双端-首尾操作数据,方便两端的数据访问 顺序容器适配器:sta ...
- 11.实战交付一套dubbo微服务到k8s集群(4)之使用Jenkins进行持续构建交付dubo服务的提供者
1.登录到jenkins,新建一个项目 2.新建流水线 3.设置保留的天数及份数 4. 添加参数 # 参数 . name: git_repo type: string description: 项目在 ...
- 解决github打不开问题
2020.06.22 使用以下方式: 在https://github.com.ipaddress.com/找到: 在https://fastly.net.ipaddress.com/github.gl ...
- 03.基于测试开发讲解和Cobertura框架介绍
首先我们先 CREATE TABLE `t_user` ( `id` int(11) NOT NULL AUTO_INCREMENT, `username` varchar(200) DEFAULT ...
