Matlab:高阶常微分三种边界条件的特殊解法（隐式Euler）

函数文件1：

 function b=F(f,x0,u,h)
       b(1,1)=x0(1)-h*x0(2)-u(1);
       b(2,1)=x0(2)+h*x0(1)^2-u(2)-h*f;

函数文件2：

 function g=Jacobian(x0,u,h)
   g(1,1)=1;
   g(1,2)=-h;
   g(2,1)=2*h*x0(1);
   g(2,2)=1; 

函数文件3：

 function x=newton_Iterative_method(f,u,h)
  % u：上一节点的数值解或者初值
  % x0 每次迭代的上一节点的数值
  % x1 每次的迭代数值
  % tol 允许误差
  % f 右端函数
 x0=u;
 tol=1e-11;
 x1=x0-Jacobian(x0,u,h)\F(f,x0,u,h);
 while (norm(x1-x0,inf)>tol)
     %数值解的2范数是否在误差范围内
     x0=x1;
     x1=x0-Jacobian(x0,u,h)\F(f,x0,u,h);
 end
 x=x1;%不动点

脚本文件：

 tic;
 clear all
 clc
 N=100;
 h=1/N;
 x=0:h:1;
 y=inline('x.^2.*sin(x).^2+2*cos(x)-x.*sin(x)');
 fun1=inline('x.*sin(x)');
 Accurate=fun1(x);
 f=y(x);
 Numerical=zeros(2,N+1);
 for i=1:N
  Numerical(1:2,i+1)=newton_Iterative_method(f(i+1),Numerical(1:2,i),h);
 end
 error=Numerical(1,:)-Accurate;
 subplot(1,3,1)
 plot(x,Accurate);
 xlabel('x');
 ylabel('Accurate');
 grid on
 subplot(1,3,2)
 plot(x,Numerical(1,:));
 xlabel('x');
 ylabel('Numerical');
 grid on
 subplot(1,3,3)
 plot(x,error);
 xlabel('x');
 ylabel('error');
 grid on
 toc;

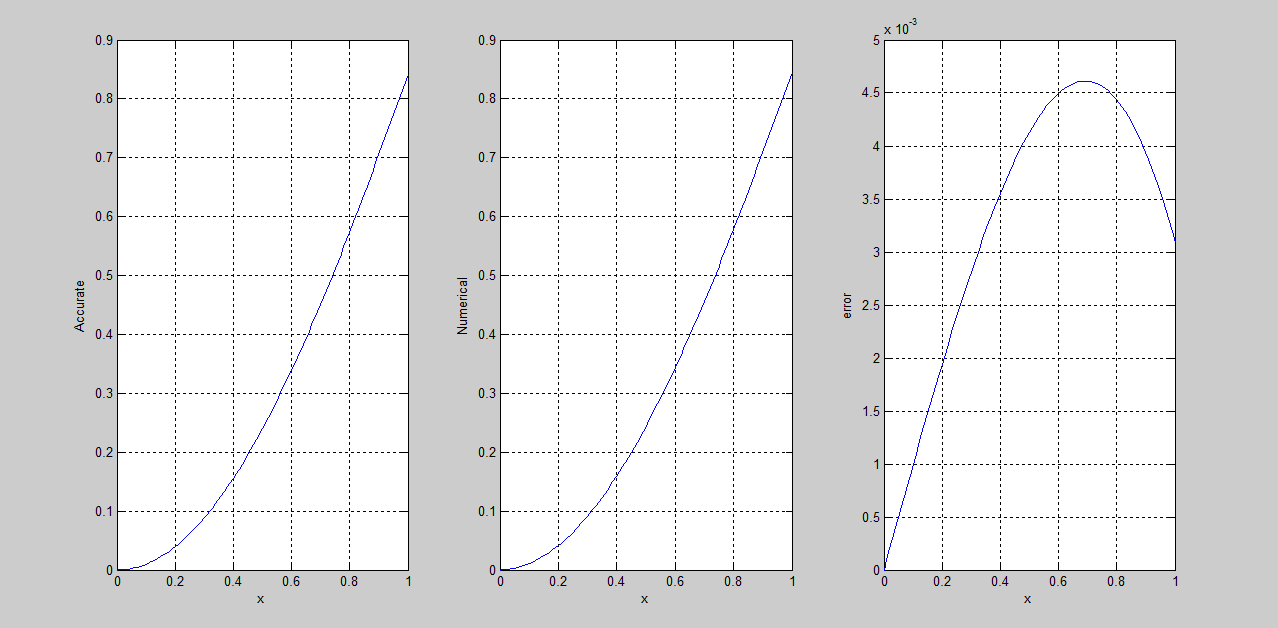
效果图：