正则化，L1，L2

机器学习中在为了减小loss时可能会带来模型容量增加，即参数增加的情况，这会导致模型在训练集上表现良好，在测试集上效果不好，也就是出现了过拟合现象。为了减小这种现象带来的影响，采用正则化。正则化，在减小训练样本误差的同时，限制参数的增长，限制参数过多或者过大，从而提高模型的泛化性。

1. L1 正则化

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

2. L2 正则化

L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

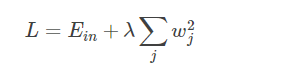
L1范式和L2范式的区别

(1) L1范式是对应参数向量绝对值之和

(2) L1范式具有稀疏性

(3) L1范式可以用来作为特征选择，并且可解释性较强（这里的原理是在实际Loss function 中都需要求最小值，根据L1的定义可知L1最小值只有0，故可以通过这种方式来进行特征选择）

(4) L2范式是对应参数向量的平方和，再求平方根

(5) L2范式是为了防止机器学习的过拟合，提升模型的泛化能力

L2正则 对应的是加入2范数，使得对权重进行衰减，从而达到惩罚损失函数的目的，防止模型过拟合。保留显著减小损失函数方向上的权重，而对于那些对函数值影响不大的权重使其衰减接近于0。相当于加入一个gaussian prior。
L1正则 对应得失加入1范数，同样可以防止过拟合。它会产生更稀疏的解，即会使得部分权重变为0，达到特征选择的效果。相当于加入了一个laplacean prior。