QT下过多点的曲线绘制

绘制过多点的曲线意义重大。但通过试验，QT的PainterPath不是很如意。当多段曲线围成一个区域时，PainterPath内并不包含该区域的所有面积，只包含曲线和其弦构成的面积。

为了解决这一问题，采用如下方法：

1. 生成自己的bezier曲线点集

2. 将多个bezier曲线头尾相联，形成整个polygon的点集

3. 将这个polygon放入一个PainterPath，然后绘制；

4. 这个PainterPath返回留待下次使用。

下面是代码：

1. 头文件graphic.h

#ifndef GRAPHIC_H

#define GRAPHIC_H

#include <QPainter>

#include <QPoint>

#include <QColor>

#include <QVector>

//step是步长，即t每次的递增量，traceSet返回本曲线的所有生成点

void getBezier3(const QPointF& startPos, const QPointF& controlPos1, const QPointF& controlPos2, const QPointF& endPos,

                const double step, QVector<QPointF>& traceSet);

//画一个多边形的外接曲线，points是多边形的顶点集合，方向是CCW或CW；k_c是连接处的尖锐度，越大越光滑，通常选0.6；path是返回量，它是一个包含了外接曲线所有点的多边形区域，可用于

//测试一个点是否在这个区域内，或两个区域是否相交等，还可以完成path的绘制。

void drawEncloseCurve(QPainter& painter, const QVector<QPoint>& points, float k_c, const QColor& color, int strokWidth, QPainterPath& path);

#endif // GRAPHIC_H

2. 绘制实现graphic.cpp

#include "graphic.h"

//求两点距离

double distance(const QPoint& p1, const QPoint& p2)

{

        return sqrt(((p1.x() - p2.x()) * (p1.x() - p2.x()) + (p1.y() - p2.y()) * (p1.y() - p2.y())));

}

//根据比例调整点的位置

QPoint ratioPointConvert(const QPoint& p1, const QPoint& p2, const double ratio)

{

        QPoint p;

        p.setX((int) (ratio * (p1.x() - p2.x()) + p2.x()));

        p.setY((int) (ratio * (p1.y() - p2.y()) + p2.y()));

        return p;

}

void getBezier3(const QPointF& startPos, const QPointF& controlPos1, const QPointF& controlPos2, const QPointF& endPos,

                const double step, QVector<QPointF>& traceSet)

{

    double t = 0.0;

    double x_t, y_t;

    while (t <= 1.0) {

        x_t = startPos.x() * (1 - t) * (1 - t) * (1 - t) + 3 * controlPos1.x() * t * (1 - t) * (1 - t) + 3 * controlPos2.x() * t * t * (1 - t) + endPos.x() * t * t * t;

        y_t = startPos.y() * (1 - t) * (1 - t) * (1 - t) + 3 * controlPos1.y() * t * (1 - t) * (1 - t) + 3 * controlPos2.y() * t * t * (1 - t) + endPos.y() * t * t * t;

        traceSet.push_back(QPointF(x_t, y_t));

        t += step;

    }

}

void drawEncloseCurve(QPainter& painter, const QVector<QPoint>& points, float k_c, const QColor& color, int strokWidth, QPainterPath& path)

{

    //path.clear();

    int size = points.size();

    QVector<QPoint> midpoints;

    // 计算中点

    for(int i = 0; i < size; i++)

    {

        int j = (i + 1) % size;

        midpoints.push_back(QPoint((points[i].x() + points[j].x()) / 2, (points[i].y() + points[j].y()) / 2));

    }

    // 计算比例点

    QVector<QPoint> ratioPoints;

    for(int i = 0; i < size; i++)

    {

        int j = (i + 1) % size;

        int m = (i + 2) % size;

        double l1 = distance(points[i], points[j]);

        double l2 = distance(points[j], points[m]);

        double ratio = l1 / (l1 + l2);

        ratioPoints.push_back(ratioPointConvert(midpoints[i], midpoints[j], ratio));

    }

    // 移动线段，计算控制点

    QVector<QPoint> controlPoints;

    for (int i = 0; i < size; i++)

    {

        QPoint ratioPoint = ratioPoints[i];

        QPoint verPoint = points[(i + 1) % size];

        int dx = ratioPoint.x() - verPoint.x();

        int dy = ratioPoint.y() - verPoint.y();

        QPoint controlPoint1 = QPoint(midpoints[i].x() - dx, midpoints[i].y() - dy);

        QPoint controlPoint2 = QPoint(midpoints[(i + 1) % size].x() - dx, midpoints[(i + 1) % size].y() - dy);

        controlPoints.push_back(ratioPointConvert(controlPoint1, verPoint, k_c));

        controlPoints.push_back(ratioPointConvert(controlPoint2, verPoint, k_c));

    }

    // 用三阶贝塞尔曲线连接顶点

    //QPainterPath path;

    QVector<QPointF> polypoints;

    QPen pen;

    pen.setColor(color);

    pen.setWidth(strokWidth);

    pen.setCapStyle(Qt::RoundCap);

    pen.setJoinStyle(Qt::RoundJoin);

    painter.setPen(pen);

    for (int i = 0; i < size; i++)

    {

        QPoint startPoint = points[i];

        QPoint endPoint = points[(i + 1) % size];

        QPoint controlPoint1 = controlPoints[(i * 2 + controlPoints.size() - 1) % controlPoints.size()];

        QPoint controlPoint2 = controlPoints[(i * 2) % controlPoints.size()];

//        path.moveTo(startPoint.x(), startPoint.y());

//        path.cubicTo(controlPoint1.x(), controlPoint1.y(), controlPoint2.x(), controlPoint2.y(), endPoint.x(), endPoint.y());

        QVector<QPointF> bezier;

        getBezier3(startPoint, controlPoint1, controlPoint2, endPoint, 0.01, bezier);

        bezier.removeLast();

        polypoints += bezier;

    }

    QPolygonF poly(polypoints);

    path.addPolygon(poly);

    painter.drawPath(path);

}

3. 测试（mainwindow.cpp）

测试时发现了问题：当Qdebug()<< 输入中文时，调试直接跳走，无法继续步进，但如果改成英文，则没有问题。

void MainWindow::paintEvent(QPaintEvent *event)

{

    QPainter painter(this);

    //绘制封闭的外接曲线

    painter.setRenderHint(QPainter::Antialiasing, true);

    QVector<QPoint> points;

    points.push_back(QPoint(200, 200));

    points.push_back(QPoint(400, 100));

    points.push_back(QPoint(600, 200));

    points.push_back(QPoint(400, 400));

    drawEncloseCurve(painter, points, 0.6, QColor(Qt::black), 2, npath);

    painter.save();

    painter.translate(400, 0);

    painter.fillPath(npath, QBrush(Qt::green));

    painter.restore();
｝

测试鼠标是否在这个区域中

void MainWindow::mousePressEvent(QMouseEvent *event)

{

    if(event->button() == Qt::LeftButton)

    {

        QPointF p = event->pos();

        if(npath.contains(p))

            qDebug() << ("you hit it path");

        //通过试验，有时用npath测试无效，但poly总是有效

        QPolygonF poly = npath.toFillPolygon();

        if(poly.containsPoint(p, Qt::WindingFill))

        {

            qDebug() << ("you hit it poly");

            startDrawing = false;

        }

        else

        {

            startDrawing = true;

            startPos = event->pos();

        }

    }

}

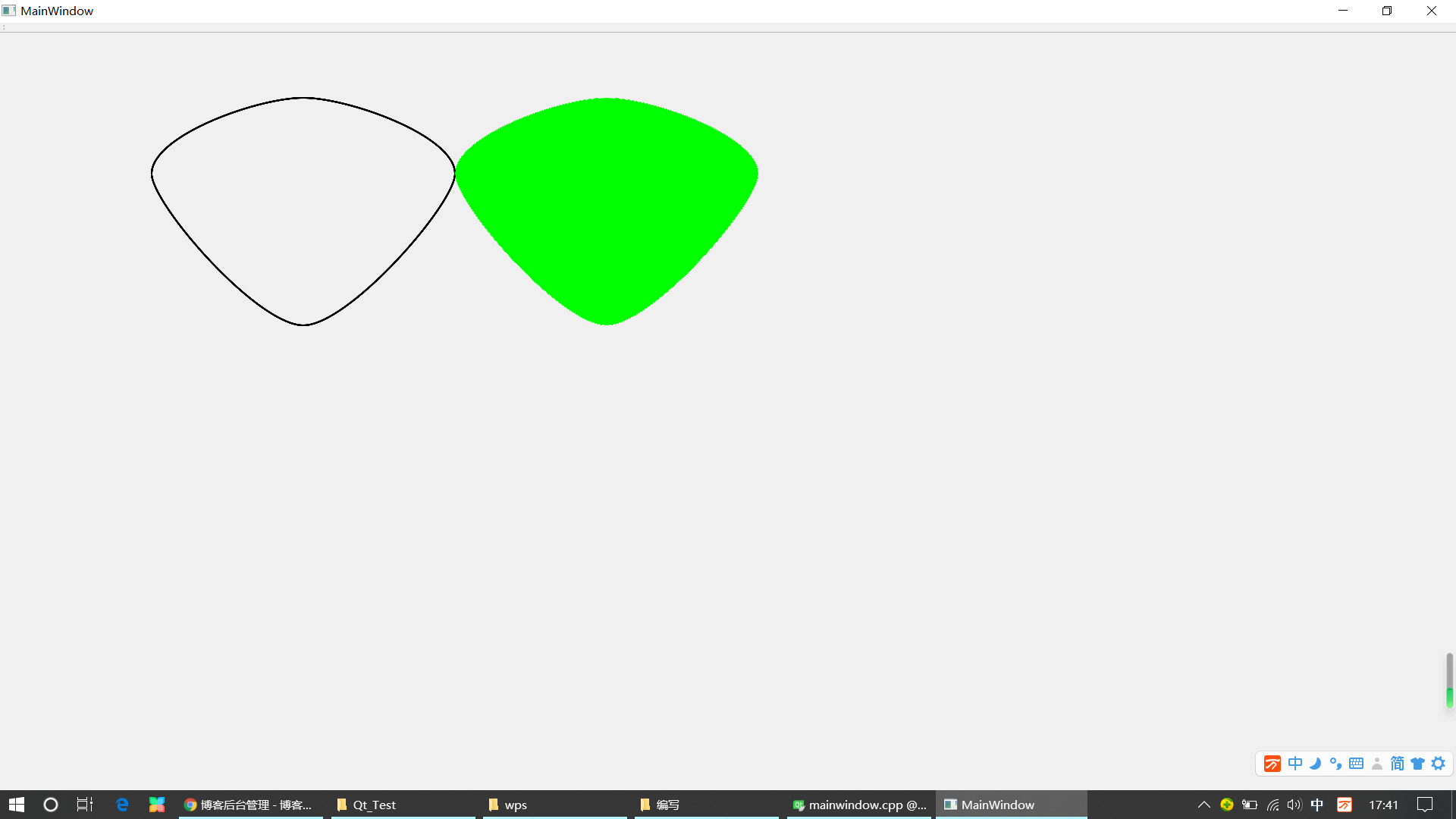
4.结果：
通过四个点的封闭曲线，并通过了鼠标选取测试