LeetCode40.组合总和II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:

[

  [1, 7],

  [1, 2, 5],

  [2, 6],

  [1, 1, 6]

]

示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:

[

  [1,2,2],

  [5]

]

思路

这道题目和[LeetCode39. 组合总和 - Tomorrowland_D - 博客园 (cnblogs.com)]()如下区别：

本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的，而[LeetCode39. 组合总和 - Tomorrowland_D - 博客园 (cnblogs.com)]()是无重复元素的数组candidates

最后本题和[LeetCode39. 组合总和 - Tomorrowland_D - 博客园 (cnblogs.com)]()要求一样，但是解集不能包含重复的组合。

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

我们直观的可以想到以下办法：我把所有组合求出来，再用set或者map去重，这么做很容易超时！
所以要在搜索的过程中就去掉重复组合。
这个去重为什么很难理解呢，所谓去重，其实就是使用过的元素不能重复选取。 这么一说好像很简单！
都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？
回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。
为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见candidates已经排序了）

强调一下，树层去重的话，需要对数组排序！

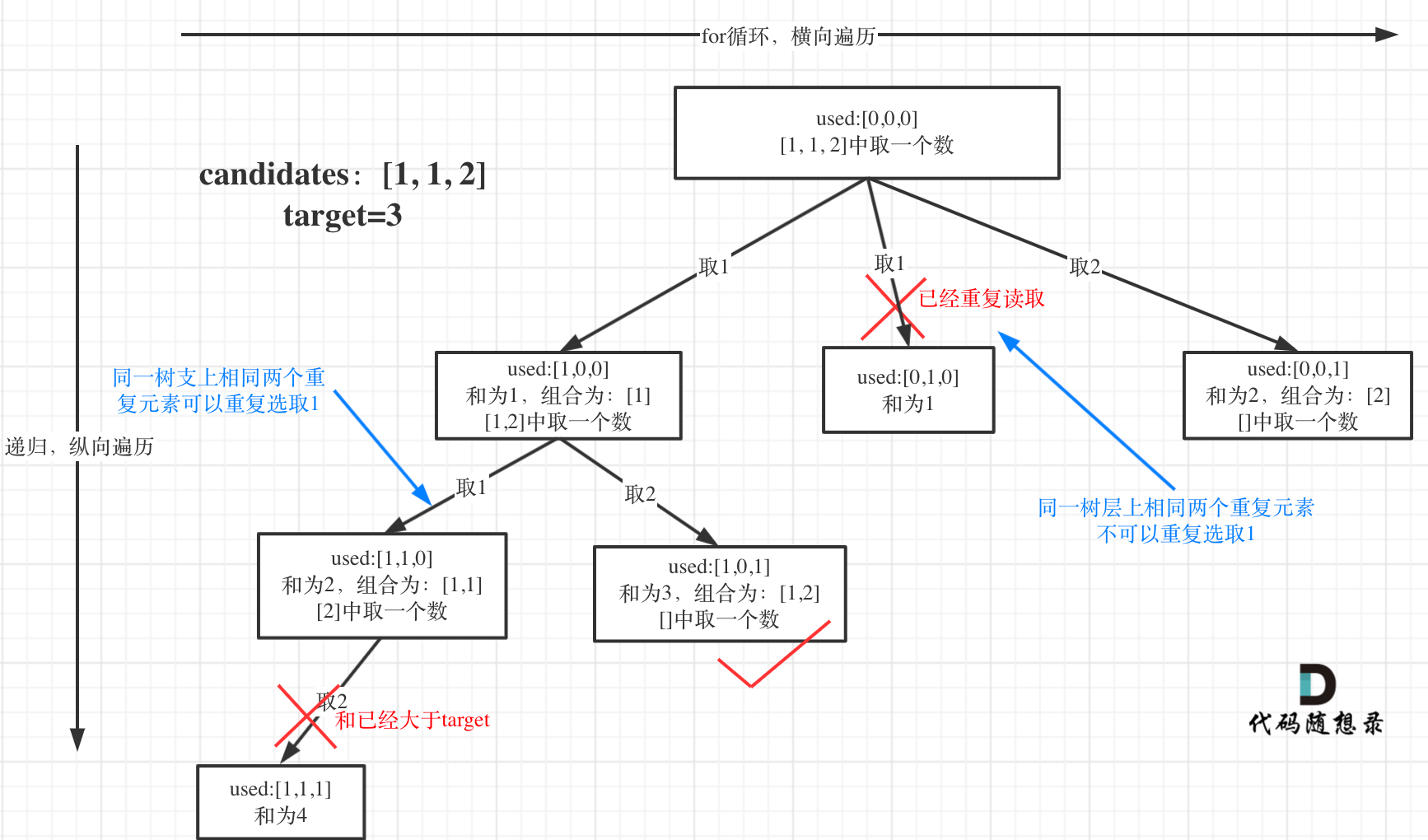
1.递归的参数

和Leetcode39组合一样，需要result存放结果，path存放单条路径
sum来存放当前的所有和
startindex来标志当前遍历的位置
还需要一个used数组来用于去重，在下面会重点介绍去重！！！

2.递归的结束条件

与上题一样，当sum＞=targetSum就返回，如果等于，我们就收集结果

3.单层搜索的逻辑

这里与LeetCode39.组合总和最大的不同就是要去重了。

前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

这块比较抽象，如图：

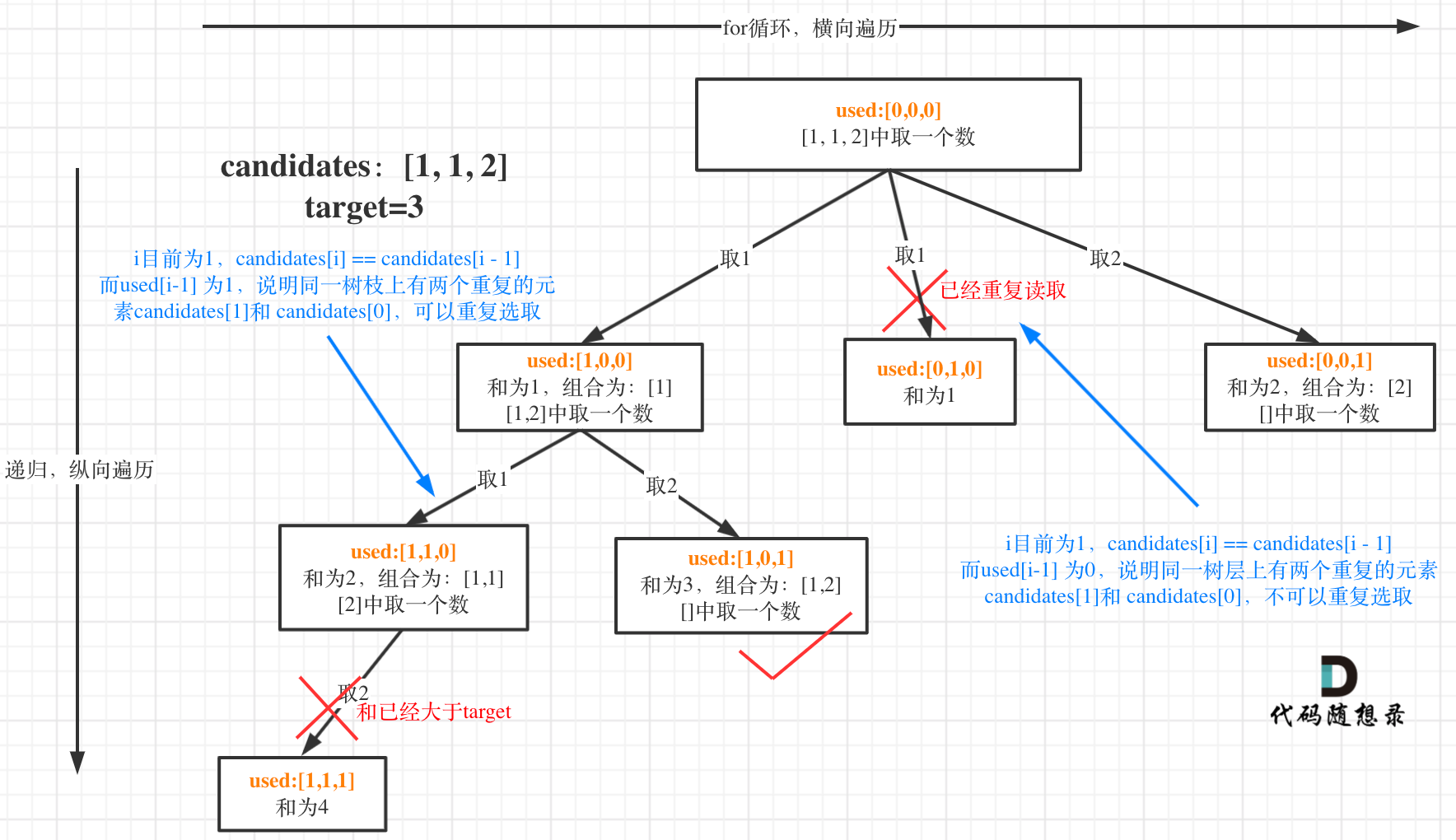
我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示

单层递归的代码如下：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {

    // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过

    // used[i - 1] == false，说明同一树层candidates[i - 1]使用过

    // 要对同一树层使用过的元素进行跳过

    if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {

        continue;

    }

    sum += candidates[i];

    path.push_back(candidates[i]);

    used[i] = true;

    backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1：这里是i+1，每个数字在每个组合中只能使用一次

    used[i] = false;

    sum -= candidates[i];

    path.pop_back();

}

代码：

class Solution {

public:

	vector<int> path;

	vector<vector<int> > result;

	void backtracking(vector<int> candidates, int targetSum, int sum, int startindex, vector<bool>& used) {

		if (sum >= targetSum) {

			if (sum == targetSum) result.push_back(path);

			return;

		}

		//这里的剪枝过程在组合总和中有讲到过！

		for (int i = startindex; i < candidates.size() && sum + candidates[i]<=targetSum; i++) {

			//如果是同一层的相同元素，就去重！也就是跳过本轮循环

            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过

            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过

            // 要对同一树层使用过的元素进行跳过

			if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0) continue;

			sum += candidates[i];

			path.push_back(candidates[i]);

			used[i] = 1;

			//要注意这里是i+1，与之前讲解的组合总和不同，这里不能够选取重复的元素

			backtracking(candidates, targetSum, sum, i + 1, used);

			sum -= candidates[i];

			path.pop_back();

			//回溯的时候将之前使用过的元素置为0，标志着这是同一层的元素（树层），而不是树枝上的元素

			used[i] = 0;

		}

	}

	vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {

		path.clear(); result.clear();

		if (candidates.size() == 0) return result;

		vector<bool> used(candidates.size(), 0);

		//注意这里一定要排序

		sort(candidates.begin(), candidates.end());

		backtracking(candidates, target, 0, 0, used);

		return result;

	}

};

注意：

本文中还多次引用到了作者代码随想录的原图，想要深入了解的可以关注原作者，阅读原作者的文章！[代码随想录 (programmercarl.com)]()