[转]Poisson Distribution

Poisson Distribution

Given a Poisson process, the probability of obtaining exactly 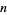successes in 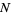trials is given by the limit of a binomial distribution

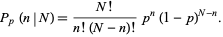(1)

Viewing the distribution as a function of the expected number of successes

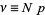(2)

instead of the sample size 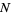for fixed 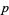, equation (2) then becomes

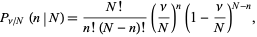(3)

Letting the sample size 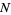become large, the distribution then approaches

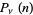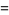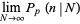			(4)
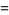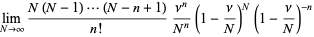			(5)
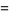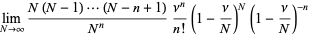			(6)
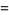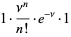			(7)
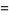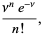			(8)

which is known as the Poisson distribution (Papoulis 1984, pp. 101 and 554; Pfeiffer and Schum 1973, p. 200). Note that the sample size 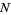has completely dropped out of the probability function, which has the same functional form for all values of .

The Poisson distribution is implemented in the Wolfram Language as PoissonDistribution[mu].

As expected, the Poisson distribution is normalized so that the sum of probabilities equals 1, since

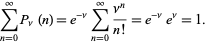(9)

The ratio of probabilities is given by

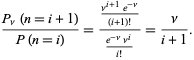(10)

The Poisson distribution reaches a maximum when

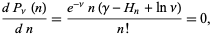(11)

where 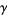is the Euler-Mascheroni constant and 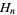is a harmonic number, leading to the transcendental equation

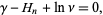(12)

which cannot be solved exactly for .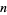

The moment-generating function of the Poisson distribution is given by

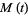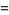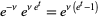			(13)
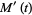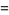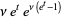			(14)
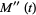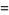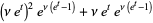			(15)
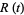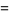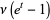			(16)
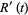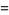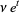			(17)
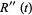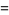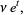			(18)

so

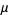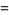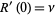			(19)
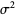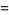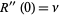			(20)

(Papoulis 1984, p. 554).

The raw moments can also be computed directly by summation, which yields an unexpected connection with the Bell polynomial 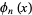and Stirling numbers of the second kind,

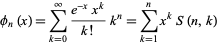(21)

known as Dobiński's formula. Therefore,

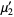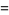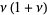			(22)
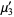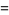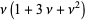			(23)
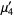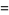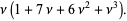			(24)

The central moments can then be computed as

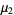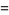			(25)
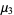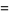			(26)
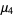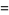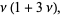			(27)

so the mean, variance, skewness, and kurtosis are

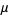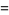			(28)
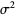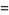			(29)
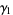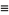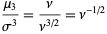			(30)
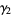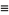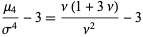			(31)
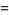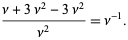			(32)

The characteristic function for the Poisson distribution is

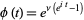(33)

(Papoulis 1984, pp. 154 and 554), and the cumulant-generating function is

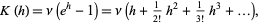(34)

so

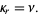(35)

The mean deviation of the Poisson distribution is given by

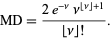(36)

The Poisson distribution can also be expressed in terms of

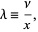(37)

the rate of changes, so that

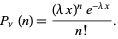(38)

The moment-generating function of a Poisson distribution in two variables is given by

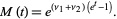(39)

If the independent variables 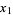, , 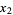..., 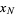have Poisson distributions with parameters 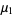, , 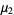..., 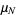, then

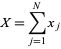(40)

has a Poisson distribution with parameter

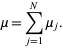(41)

This can be seen since the cumulant-generating function is

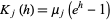(42)

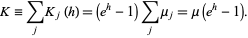(43)

A generalization of the Poisson distribution has been used by Saslaw (1989) to model the observed clustering of galaxies in the universe. The form of this distribution is given by

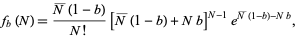(44)

where 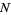is the number of galaxies in a volume 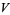, , 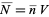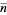is the average density of galaxies, and 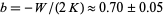, with 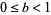is the ratio of gravitational energy to the kinetic energy of peculiar motions, Letting 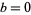gives

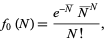(45)

which is indeed a Poisson distribution with 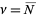. Similarly, letting 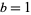gives .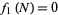

SEE ALSO: Binomial Distribution, Erlang Distribution, Poisson Process, Poisson Theorem

 

REFERENCES:

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 532, 1987.

Grimmett, G. and Stirzaker, D. Probability and Random Processes, 2nd ed. Oxford, England: Oxford University Press, 1992.

Papoulis, A. "Poisson Process and Shot Noise." Ch. 16 in Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 554-576, 1984.

Pfeiffer, P. E. and Schum, D. A. Introduction to Applied Probability. New York: Academic Press, 1973.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 209-214, 1992.

Saslaw, W. C. "Some Properties of a Statistical Distribution Function for Galaxy Clustering." Astrophys. J. 341, 588-598, 1989.

Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 111-112, 1992.

 

Referenced on Wolfram|Alpha: Poisson Distribution

 

CITE THIS AS:

Weisstein, Eric W. "Poisson Distribution." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PoissonDistribution.html

1重 0-1分布

N重 二项分布 ，  系数为阶乘降/阶乘增， 从0开始

无限重 v=Np,  泊松分析， 先确定N,再确定对应的p, 再得v,   此时才有泊松分布公式可用