poj 1696 Space Ant（模拟+叉积）

Space Ant

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3840		Accepted: 2397

Description

The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:

1. It can not turn right due to its special body structure.
2. It leaves a red path while walking.
3. It hates to pass over a previously red colored path, and never does that.

The pictures transmitted by the Discovery space ship depicts that
plants in the Y1999 grow in special points on the planet. Analysis of
several thousands of the pictures have resulted in discovering a magic
coordinate system governing the grow points of the plants. In this
coordinate system with x and y axes, no two plants share the same x or y.

An M11 needs to eat exactly one plant in each day to stay alive.
When it eats one plant, it remains there for the rest of the day with no
move. Next day, it looks for another plant to go there and eat it. If
it can not reach any other plant it dies by the end of the day. Notice
that it can reach a plant in any distance.

The problem is to find a path for an M11 to let it live longest.

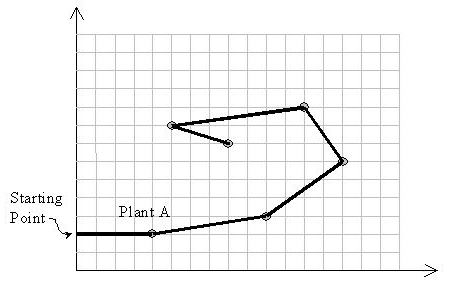
Input is a set of (x, y) coordinates of plants. Suppose A with the
coordinates (xA, yA) is the plant with the least y-coordinate. M11
starts from point (0,yA) heading towards plant A. Notice that the
solution path should not cross itself and all of the turns should be
counter-clockwise. Also note that the solution may visit more than two
plants located on a same straight line.

Input

The
first line of the input is M, the number of test cases to be solved (1
<= M <= 10). For each test case, the first line is N, the number
of plants in that test case (1 <= N <= 50), followed by N lines
for each plant data. Each plant data consists of three integers: the
first number is the unique plant index (1..N), followed by two positive
integers x and y representing the coordinates of the plant. Plants are
sorted by the increasing order on their indices in the input file.
Suppose that the values of coordinates are at most 100.

Output

Output
should have one separate line for the solution of each test case. A
solution is the number of plants on the solution path, followed by the
indices of visiting plants in the path in the order of their visits.

Sample Input

2
10
1 4 5
2 9 8
3 5 9
4 1 7
5 3 2
6 6 3
7 10 10
8 8 1
9 2 4
10 7 6
14
1 6 11
2 11 9
3 8 7
4 12 8
5 9 20
6 3 2
7 1 6
8 2 13
9 15 1
10 14 17
11 13 19
12 5 18
13 7 3
14 10 16

Sample Output

10 8 7 3 4 9 5 6 2 1 10
14 9 10 11 5 12 8 7 6 13 4 14 1 3 2

Source

Tehran 1999

【思路】

模拟+叉积

模拟行走过程，利用叉积判断。时间复杂度为O(n²logn)

【代码】

 #include<cmath>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define FOR(a,b,c) for(int a=(b);a<=(c);a++)
 using namespace std;

 const int N = +;
 const double eps = 1e-;
 int dcmp(double x) {
     if(fabs(x)<eps) return ; else return x<? -:;
 }

 struct Pt {
     double x,y; int r;
     Pt (double x=,double y=) :x(x),y(y) {};
 };
 typedef Pt vec;

 vec operator - (Pt a,Pt b) { return vec(a.x-b.x,a.y-b.y); }
 double cross(vec a,vec b) { return a.x*b.y-a.y*b.x; }
 double dist(Pt a,Pt b) {
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 }

 Pt p[N];
 int n,pos;

 bool cmp(Pt a,Pt b) {
     double c=cross(a-p[pos],b-p[pos]);
     if(dcmp(c)==) return dist(p[pos],a) < dist(p[pos],b);
     else if(dcmp(c)<) return ; else return ;
 }

 int main() {
     int T;
     scanf("%d",&T);
     while(T--) {
         scanf("%d",&n);
         FOR(i,,n-) {
             scanf("%d%lf%lf",&p[i].r,&p[i].x,&p[i].y);
             if(p[i].y<p[].y || p[i].y==p[].y && p[i].x<p[].x) swap(p[],p[i]);
         }
         pos=;
         FOR(i,,n-)
             sort(p+i,p+n,cmp) , pos++;
         printf("%d",n);
         FOR(i,,n-)
             printf(" %d",p[i].r);
         putchar('\n');
     }
     return ;
 }