【NLP_Stanford课堂】语言模型4
平滑方法:
1. Add-1 smoothing
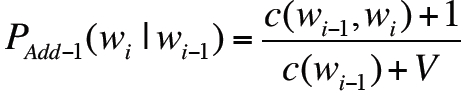
2. Add-k smoothing

设m=1/V,则有
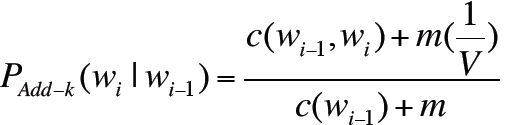
从而每一项可以跟词汇表的大小相关
3. Unigram prior smoothing
将上式中的1/v换成unigram概率P(wi),则有:

其是插值的一种变体,其将某种unigram概率加入到bigram的计算中。
4. Good-Turing Smoothing
大部分平滑算法比如Good-Turing、Kneser-Ney、Witten-Bell采用的主要思想是用之前已知的数据的计数来预测未知的数据的计数,旨在将未知的0值用其他数值替代。
下面是具体方法:

表示频率c出现的次数,然后将其应用到Good-Turing平滑算法中,如下:
假设你在钓鱼,然后抓到了:
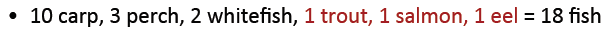
1)下一条鱼是trout的概率是多少?
答:1/18
2)下一条鱼是新的品种的概率是多少?
答:3/18,因为N1=3
3)下一条鱼是trout的概率是多少
答:小于1/18,因为还有一部分概率3/18是留给新的品质的鱼的。具体数值使用Good Turing方法计算。
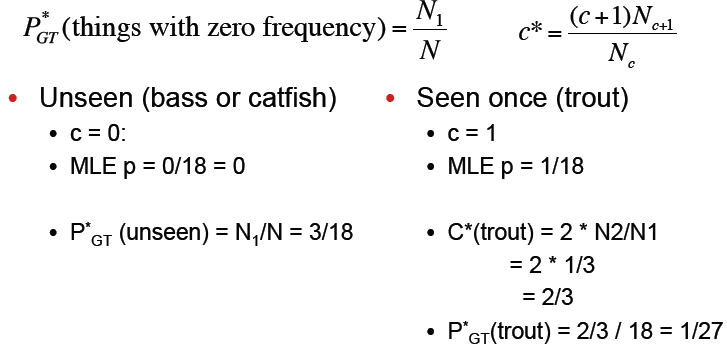
MLE:最大似然概率
具体方法:
设有一个大小为c的训练集,然后从c个词中抽取一个词作为留存数据,则原数据集大小变为c-1,然后在原训练集中抽取另一词作为留存数据,迭代重复抽取过程,重复c次,则得到c个c-1大小的训练集和大小为1的留存数据集,如下:
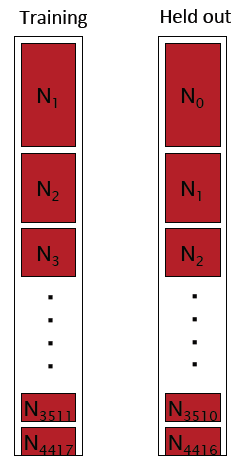
如此,假设每个留存数据在原训练集中出现r次,则抽取之后该留存数据在对应现数据集中出现r-1次,则原Nr即计数为r的词的频次需要减一,而Nr-1即计数为r-1的词的频次需要加1,从而有以上对应内容,即现对应Nr-1的内容为原Nr的内容。
那么
1)有多少比例的留存数据在训练集中是不可见的:N1/C
2)有多少比例的留存书籍在训练集中出现了k次: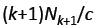
所以我们预计会出现 个词,其出现频次在训练集中为k。
个词,其出现频次在训练集中为k。
又因为在训练数据集中出现k次的词一共有Nk个,所以每个词出现的概率为: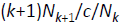
或者写作: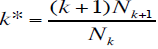
但是有一个问题,可能Nk+1与Nk的值差的非常大,那么以上计算方法就容易不准确。
实际上语料库中Nk的分布可能如下所示:
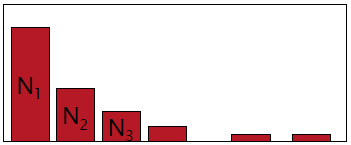
可能出现频次非常大的N4417中只有一个“the”这个词。
所以在Simple Good-Turing中在计数是除了最开始的几项,后续的采用合适的拟合曲线来表征,如下:
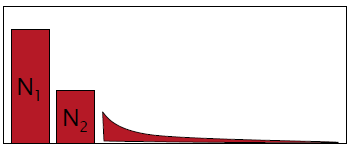
5. Kneser-Ney Smoothing
上述Good-Turing Smoothing方法中,对于每一项的计数做了一下调整:
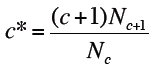 ,从而有:
,从而有:
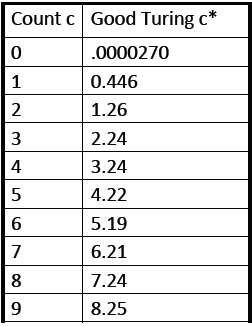
可以发现每一项的新值其实差不多为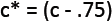
即差值是固定的,那么我们可以直接应用这种固定的差值(也称之为折扣),称之为absolute discounting绝对折扣法。
· Absolute Discounting Interpolation

d是一个固定的数值,即折扣。但是关键在于应用unigram的项是否恰当,所以有:
· Kneser-Ney 概率forunigram
当我们要预测下一个词的时候,比如:I cant see withon my reading ______
实际上应该是glasses,但是如果单单按照unigram频次的话,Francisco更有可能,因为其频次更高。然后Fancisco一般是紧随着San出现的,所以unigram只有在我们不知道bigram的时候才有用.
所以我们不应该只简单地问P(w):"是w这个词的可能性是多少",而是应该问 :“w能组成一种新的‘延续’的可能性是多少”,那么如何计算这个概率呢?
:“w能组成一种新的‘延续’的可能性是多少”,那么如何计算这个概率呢?
· 对于每个词,计算它紧跟着另一个词所组成的不同的bigram类型的数目
· 每个第一次出现的bigram即是一种新的‘延续’,其概率与能跟w组成bigram的词的集合大小成比例:
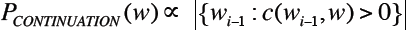
再用整体bigram类型数目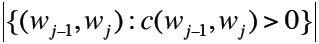 做正则化:
做正则化:

在Kneser-Ney Smoothing中写作:
与w组成bigram的前驱单词数目=
用所有bigram数目做正则化,则有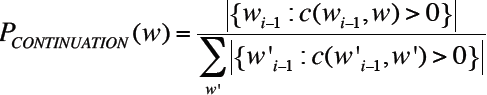
结合以上absolute discounting和Kneser-Ney 概率forunigram,则有:
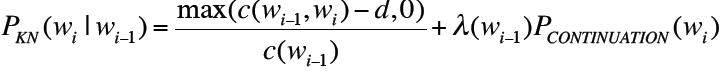
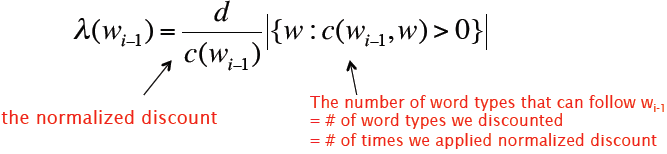
以上是Kneser-Ney Smoothing对于bigram的计算方式,以下则是对通用N-gram的计算方法:
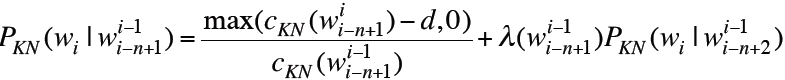
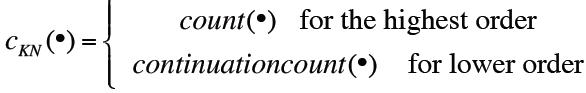

【NLP_Stanford课堂】语言模型4的更多相关文章
- 【NLP_Stanford课堂】语言模型3
一.产生句子 方法:Shannon Visualization Method 过程:根据概率,每次随机选择一个bigram,从而来产生一个句子 比如: 从句子开始标志的bigram开始,我们先有一个( ...
- 【NLP_Stanford课堂】语言模型2
一.如何评价语言模型的好坏 标准:比起语法不通的.不太可能出现的句子,是否为“真实”或"比较可能出现的”句子分配更高的概率 过程:先在训练数据集上训练模型的参数,然后在测试数据集上测试模型的 ...
- 【NLP_Stanford课堂】语言模型1
一.语言模型 旨在:给一个句子或一组词计算一个联合概率 作用: 机器翻译:用以区分翻译结果的好坏 拼写校正:某一个拼错的单词是这个单词的概率更大,所以校正 语音识别:语音识别出来是这个句子的概率更大 ...
- 【NLP_Stanford课堂】文本分类1
文本分类实例:分辨垃圾邮件.文章作者识别.作者性别识别.电影评论情感识别(积极或消极).文章主题识别及任何可分类的任务. 一.文本分类问题定义: 输入: 一个文本d 一个固定的类别集合C={c1,c2 ...
- 【NLP_Stanford课堂】拼写校正
在多种应用比如word中都有拼写检查和校正功能,具体步骤分为: 拼写错误检测 拼写错误校正: 自动校正:hte -> the 建议一个校正 建议多个校正 拼写错误类型: Non-word Err ...
- 【NLP_Stanford课堂】情感分析
一.简介 实例: 电影评论.产品评论是positive还是negative 公众.消费者的信心是否在增加 公众对于候选人.社会事件等的倾向 预测股票市场的涨跌 Affective States又分为: ...
- 【NLP_Stanford课堂】文本分类2
一.实验评估参数 实验数据本身可以分为是否属于某一个类(即correct和not correct),表示本身是否属于某一类别上,这是客观事实:又可以按照我们系统的输出是否属于某一个类(即selecte ...
- 【NLP_Stanford课堂】最小编辑距离
一.什么是最小编辑距离 最小编辑距离:是用以衡量两个字符串之间的相似度,是两个字符串之间的最小操作数,即从一个字符转换成另一个字符所需要的操作数,包括插入.删除和置换. 每个操作数的cost: 每个操 ...
- 【NLP_Stanford课堂】句子切分
依照什么切分句子——标点符号 无歧义的:!?等 存在歧义的:. 英文中的.不止表示句号,也可能出现在句子中间,比如缩写Dr. 或者数字里的小数点4.3 解决方法:建立一个二元分类器: 检查“.” 判断 ...
随机推荐
- @media响应式布局
@media可以根据屏幕尺寸调节布局 @media screen and (min-width:100px) and (max-width:200px){ div { color:red; } } 在 ...
- hive DML
1.load files into tables 把文件中的数据加载到表中(表必须先建好) 语法是: load data [local] inpath 'filepath' [overwrite] i ...
- 关于halo博客系统的使用踩坑——忘记登录密码
踩坑: halo系统可以直接通过运行jar -jar halo-0.0.3.jar跑起来,也可以通过导入IDE然后运行Application的main方法跑起系统. h2数据库访问路径:http:// ...
- Kettle 中生成随机数 或者GUID唯一标识符
添加步骤 "生成随机数" 英文名字叫 "Generate Random Value" 如下图..选择UUID..
- Case When ELSE END语句
一.简介.Case When ELSE END共有两种用法: 说实话,这种就是数据库版的switch语句,但是只是形式上很像,实际上还是有差别的!!! Create Table Test6( ...
- Jmeter测试计划中的元素
测试计划中的元素(elements of a test plan) 本节描述测试计划不同的部分. 最小测试将包括测试计划.线程组和一个或多个采样器. 1 测试计划(Test Plan) 测试计划对象有 ...
- datepicker97切换年月日再连续点击下拉中日期的bug出现问题
解决办法: function wdateOption(fmt){ if(fmt===undefined){fmt="yyyy-MM-dd"} return{ dateFmt:fmt ...
- JavaScript数组forEach循环
JavaScript数组forEach循环 今天写JavaScript代码把forEach循环数组忘记写法了,在此记录一下以防止未来忘记. let a = [1, 2, 3]; a.forEach(f ...
- 收集整理mysql数据库设计规范与原则
1. 数据库命名规范 采用26个英文字母(区分大小写)和0-9的自然数(经常不需要)加上下划线'_'组成;命名简洁明确(长度不能超过30个字符);例如:user, stat, log, 也可以wifi ...
- WPF的DatePicker--日期选择器
1. 日期选择器 DatePicker, 如图: 点击打开后显示如下: 2. 关键属性 SelectedDate SelectedDate属性, DateTime? 类型(可为空的DateTime类型 ...
