PID控制器开发笔记之十：步进式PID控制器的实现

　　对于一般的PID控制系统来说，当设定值发生较大的突变时，很容易产生超调而使系统不稳定。为了解决这种阶跃变化造成的不利影响，人们发明了步进式PID控制算法。

1、步进式PID的基本思想

　　所谓步进式PID算法，实际就是在设定值发生阶跃变化时，不直接对阶跃信号进行响应，而是在一定的时间内逐步改变设定值，直至使设定值达到目标值。这种逐步改变设定值的办法使得对象运行平稳。适用于高精度伺服系统的位置跟踪。

　　佷显然，这一方法并未改变PID控制器本身，而是对设定值做了前期处理。所以其结构框图与控制方程与其他的PID控制算法是一致的。

　　为了对设定值做必要处理，以使其不知快速变化，有多种方法。比较常用的是建立线性变化函数的办法。我们可以规定设定值从0-100%的变化时间为T，则可以确定设定值变化的斜率绝对值，或者说是步长。知道补偿后，我们就可以根据不常来不断修改设定值，直到目标值。可用公式描述为：

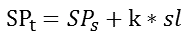
　　其中SPt为设定值目标值，SPs为设定值的起始值，sl为步长，k为步长的变化系数：

　　而控制器本身的位置型和增量型表达式都保持不变。

2、算法实现

　　步进式PID的实质是将设定值的突变修改为平缓的变化，这一处理方式在控制中有大量应用。处理设定值变化过程的流程如下所示：

　　根据这一流程我们可变写处理函数如下：

 /*步进式PID控制设定值步进处理函数*/
 float StepInProcessing(CLASSICPID vPID,float sp)
 {
   float stepIn=(vPID->maximum-vPID->minimum))*0.1;
   float kFactor=0.0;

   if(fabs(vPID->setpoint-sp)<=stepIn)
   {
     vPID->setpoint=sp;
   }
   else
   {
     if(vPID->setpoint-sp>)
     {
       kFactor=-1.0;
     }
     else if(vPID->setpoint-sp<)
     {
       kFactor=1.0;
     }
     else
     {
       kFactor=0.0;
     }
     vPID->setpoint=vPID->setpoint+k*stepIn;
   }

   return vPID->setpoint;

 }

　　有了这一处理函数后，在调用PID控制器前，先对设定值进行判断，然后将该函数的结果作为设定值给PID控制器。至于PID控制器才用前面讲述的哪种形式，根据具体应用需求和使用方便去年而定。

3、总结

　　所谓步进式实质是对设定值进行平缓变化处理，防止因为设定值的跳变而引起系统的波动。这一办法虽然能够减少阶跃跳变的干扰，但也会让系统的响应速度变慢，当然这要根据需要来处理，因为步长的选择决定了作用大小，补偿越小约平缓，相应的响应速度也越慢。

欢迎关注：