LOJ#2085 循环之美

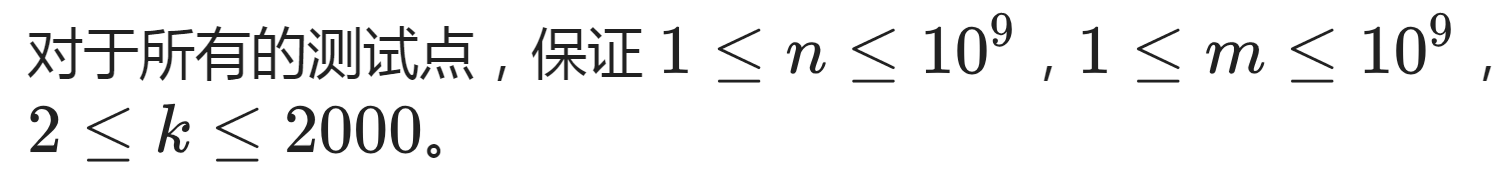
解：首先看这个纯循环到底是什么玩意.....

经过一番打表，发现纯循环小数就是分母与进制互质的既约分数。

 #include <bits/stdc++.h>

 std::bitset<> vis;

 inline bool check(int x, int y) { /// x / y
     //printf("x = %d y = %d \n", x, y);
     vis.reset();
     int rest = x % y;
     if(!rest) return true;
     int op = rest;
     vis[op] = ;
     //printf("op = %d \n", op);
     while(true) {
         rest *= ;
         int r = rest % y;
         //printf("r  = %d \n", r);
         if(vis[r]) {
             //printf("return %d = %d \n", r, op);
             return r == op;
         }
         vis[r] = ;
         rest = r;
     }
     return false;
 }

 int gcd(int a, int b) {
     if(!b) return a;
     return gcd(b, a % b);
 }

 int main() {

     int n;
     scanf("%d", &n);

     for(int i = ; i <= n; i++) {
         for(int j = ; j <= n; j++) {
             if(gcd(i, j) == ) printf("%d ", (int)check(i, j));
             else printf("  ");
         }
         puts("");
     }

     return ;
 }

打表程序

那么就有了一个很显然的O(nmlogV)的做法...直接暴力枚举然后检验。实测24分。

 #include <bits/stdc++.h>

 int gcd(int a, int b) {
     if(!b) return a;
     return gcd(b, a % b);
 }

 int main() {
     int n, m, k, ans = ;
     scanf("%d%d%d", &n, &m, &k);
     if(1ll * n * m > ) return ;
     for(int i = ; i <= m; i++) {
         if(gcd(k, i) > ) continue;
         for(int j = ; j <= n; j++) {
             ans += gcd(i, j) == ;
         }
     }
     printf("%d\n", ans);
     return ;
 }

24分暴力

然后发现最里面那句话有点像phi...仔细思考之后发现不是。

现在开始鬼畜时间...推柿子。

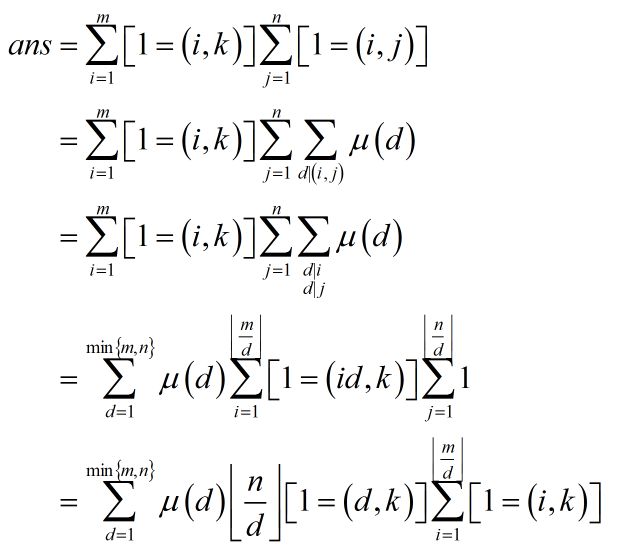
其中有两步转化，分别是把[x=1]用∑μ代替和把[1=(id,k)]用[1=(i,k)][1=(d,k)]代替。

于是考虑最后这个式子，发现有个东西[1=(a,k)]，于是设这个东西为g(x)，它的前缀和为f(x)。又令F为μ·g的前缀和。

那么答案就是下式：

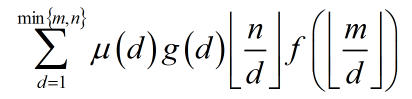
这个东西显然可以分块一波。后两项可以O(1)算，前面的可以线性预处理。于是我们有个O(n)的算法。可以获得84分。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 int miu[N], p[N], top, f[N], phi[N], n, m, k, F[N];
 bool vis[N];

 inline void getp(int n) {
     phi[] = miu[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             miu[i] = -;
             phi[i] = i - ;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             if(i % p[j] == ) {
                 //miu[i * p[j]] = 0;
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
             miu[i * p[j]] = -miu[i];
         }
     }
     return;
 }

 int gcd(int a, int b) {
     if(!b) return a;
     return gcd(b, a % b);
 }

 inline void prework() {
     for(int i = ; i <= k; i++) {
         f[i] = f[i - ] + (gcd(i, k) == );
         F[i] = F[i - ] + (f[i] - f[i - ]) * miu[i];
     }
     int len = std::min(n, m);
     for(int i = k + ; i <= len; i++) {
         f[i] = f[k] * (i / k) + f[i % k];
         F[i] = F[i - ] + (f[i] - f[i - ]) * miu[i];
     }
     return;
 }

 inline int getf(int x) {
     if(x <= k) return f[x];
     return f[k] * (x / k) + f[x % k];
 }

 int main() {
     LL ans = ;
     scanf("%d%d%d", &n, &m, &k);
     if(1ll * n * m < 1e9) {
         for(int i = ; i <= m; i++) {
             if(gcd(k, i) > ) continue;
             for(int j = ; j <= n; j++) {
                 ans += gcd(i, j) == ;
             }
         }
         printf("%lld\n", ans);
         return ;
     }
     if(n < N) {
         getp(n);
         prework();
         int len = std::min(n, m);
         for(int i = , j; i <= len; i = j + ) {
             j = std::min(n / (n / i), m / (m / i));
             /// [i, j]
             ans += 1ll * (F[j] - F[i - ]) * (n / i) * getf(m / i);
         }
         printf("%lld\n", ans);
     }
     return ;
 }

84分代码

接下来补个k = 2 / 3的部分分。严格来说应该能应付k是质数的情况，然而后面k都是合数....

推倒过程几乎跟上面一样，最后得到这个东西：

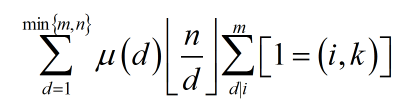
考虑怎么计算后面那个求和符号。当d和k不互质(d是k的倍数)的时候，答案显然是0。否则令t = i / d，答案就是与k互质的t个个数。这个东西我们可以用maxt - maxt / k来O(1)计算。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 int miu[N], p[N], top, f[N], phi[N], n, m, k, F[N];
 bool vis[N];

 inline void getp(int n) {
     phi[] = miu[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             miu[i] = -;
             phi[i] = i - ;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             if(i % p[j] == ) {
                 //miu[i * p[j]] = 0;
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
             miu[i * p[j]] = -miu[i];
         }
     }
     return;
 }

 int gcd(int a, int b) {
     if(!b) return a;
     return gcd(b, a % b);
 }

 inline int calc(int d) {
     if((d % k) == ) {
         return ;
     }
     d = m / d;
     return d - d / k;
 }

 inline void prework() {
     for(int i = ; i <= k; i++) {
         f[i] = f[i - ] + (gcd(i, k) == );
         F[i] = F[i - ] + (f[i] - f[i - ]) * miu[i];
     }
     int len = std::min(n, m);
     for(int i = k + ; i <= len; i++) {
         f[i] = f[k] * (i / k) + f[i % k];
         F[i] = F[i - ] + (f[i] - f[i - ]) * miu[i];
     }
     return;
 }

 inline int getf(int x) {
     if(x <= k) return f[x];
     return f[k] * (x / k) + f[x % k];
 }

 int main() {
     LL ans = ;
     scanf("%d%d%d", &n, &m, &k);
     if(1ll * n * m < 1e9) {
         for(int i = ; i <= m; i++) {
             if(gcd(k, i) > ) continue;
             for(int j = ; j <= n; j++) {
                 ans += gcd(i, j) == ;
             }
         }
         printf("%lld\n", ans);
         return ;
     }
     if((k ==  || k == ) && (n <= )) {
         getp(n);
         int len = std::min(n, m);
         for(int i = ; i <= len; i++) {
             ans += 1ll * miu[i] * (n / i) * calc(i);
         }
         printf("%lld\n", ans);
         return ;
     }
     /*if(n < N) {
         getp(n);
         prework();
         int len = std::min(n, m);
         for(int i = 1, j; i <= len; i = j + 1) {
             j = std::min(n / (n / i), m / (m / i));
             /// [i, j]
             ans += 1ll * (F[j] - F[i - 1]) * (n / i) * getf(m / i);
         }
         printf("%lld\n", ans);
     }*/
     return ;
 }

40分代码