Unique Paths leetcode java

题目：

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time.
The robot is trying to reach the bottom-right corner of the grid (marked
'Finish' in the diagram below).

How many possible unique paths are there?

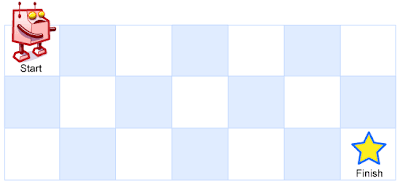
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

题解：

其实跟爬梯子挺类似的，按个就是只能往上爬，这个就是方向可以换了下。同样想法动态规划。

分析方法也一样的，想想要到最右下角。到达右下角的方法只有两个，从上面往下，和从右面往左。

利用到达终点的唯一性，就可以写出递推公式（dp[i][j]表示到坐标（i,j）的走法数量）：

dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始条件的话，当整个格子只有一行，那么到每个格子走法只有1种；只有一列的情况同理。

所以，理解的这些，代码就非常好写了。

通常来讲，我们会初始dp数组为dp[m+1][n+1]。但是这里的话，因为dp[i][j]是表示坐标点，所以这里声明dp[m][n]更容易理解。

代码如下：

 1 public static int uniquePaths(int m, int n){  
 2              if(m==0 || n==0) return 0;  
 3              if(m ==1 || n==1) return 1;  
 4               
 5             int[][] dp = new int[m][n];  
 6               
 7             //只有一行时，到终点每个格子只有一种走法  
 8             for (int i=0; i<n; i++)  
 9                 dp[0][i] = 1;  
               
             // 只有一列时，到终点每个格子只有一种走法
             for (int i=0; i<m; i++)  
                 dp[i][0] = 1;  
               
             // for each body node, number of path = paths from top + paths from left  
             for (int i=1; i<m; i++){  
                 for (int j=1; j<n; j++){  
                     dp[i][j] = dp[i-1][j] + dp[i][j-1];  
                 }  
             }  
             return dp[m-1][n-1];  
         }