二叉树的深度优先遍历与广度优先遍历 [ C++ 实现 ]

深度优先搜索算法（Depth First Search），是搜索算法的一种。是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。

当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。

如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

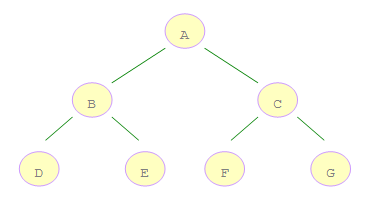
如右图所示的二叉树：

A 是第一个访问的，然后顺序是 B、D，然后是 E。接着再是 C、F、G。

那么，怎么样才能来保证这个访问的顺序呢？

分析一下，在遍历了根结点后，就开始遍历左子树，最后才是右子树。

因此可以借助堆栈的数据结构，由于堆栈是后进先出的顺序，由此可以先将右子树压栈，然后再对左子树压栈，

这样一来，左子树结点就存在了栈顶上，因此某结点的左子树能在它的右子树遍历之前被遍历。

深度优先遍历代码片段

//深度优先遍历
void depthFirstSearch(Tree root){
    stack<Node *> nodeStack;  //使用C++的STL标准模板库
    nodeStack.push(root);
    Node *node;
    while(!nodeStack.empty()){
        node = nodeStack.top();
        printf(format, node->data);  //遍历根结点
        nodeStack.pop();
        if(node->rchild){
            nodeStack.push(node->rchild);  //先将右子树压栈
        }
        if(node->lchild){
            nodeStack.push(node->lchild);  //再将左子树压栈
        }
    }
}

　　广度优先搜索算法（Breadth First Search），又叫宽度优先搜索，或横向优先搜索。

是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

如右图所示的二叉树，A 是第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。

那么，怎样才能来保证这个访问的顺序呢？

借助队列数据结构，由于队列是先进先出的顺序，因此可以先将左子树入队，然后再将右子树入队。

这样一来，左子树结点就存在队头，可以先被访问到。

广度优先遍历代码片段

//广度优先遍历
void breadthFirstSearch(Tree root){
    queue<Node *> nodeQueue;  //使用C++的STL标准模板库
    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先将左子树入队
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再将右子树入队
        }
    }
}

　　完整代码:

/**
 * <!--
 * File   : binarytree.h
 * Author : fancy
 * Email  : fancydeepin@yeah.net
 * Date   : 2013-02-03
 * --!>
 */
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <Stack>
#include <Queue>
using namespace std;
#define Element char
#define format "%c"

typedef struct Node {
    Element data;
    struct Node *lchild;
    struct Node *rchild;
} *Tree;

int index = 0;  //全局索引变量

//二叉树构造器,按先序遍历顺序构造二叉树
//无左子树或右子树用'#'表示
void treeNodeConstructor(Tree &root, Element data[]){
    Element e = data[index++];
    if(e == '#'){
        root = NULL;
    }else{
        root = (Node *)malloc(sizeof(Node));
        root->data = e;
        treeNodeConstructor(root->lchild, data);  //递归构建左子树
        treeNodeConstructor(root->rchild, data);  //递归构建右子树
    }
}

//深度优先遍历
void depthFirstSearch(Tree root){
    stack<Node *> nodeStack;  //使用C++的STL标准模板库
    nodeStack.push(root);
    Node *node;
    while(!nodeStack.empty()){
        node = nodeStack.top();
        printf(format, node->data);  //遍历根结点
        nodeStack.pop();
        if(node->rchild){
            nodeStack.push(node->rchild);  //先将右子树压栈
        }
        if(node->lchild){
            nodeStack.push(node->lchild);  //再将左子树压栈
        }
    }
}

//广度优先遍历
void breadthFirstSearch(Tree root){
    queue<Node *> nodeQueue;  //使用C++的STL标准模板库
    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先将左子树入队
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再将右子树入队
        }
    }
}

　　

/**
 * <!--
 * File   : BinaryTreeSearch.h
 * Author : fancy
 * Email  : fancydeepin@yeah.net
 * Date   : 2013-02-03
 * --!>
 */
#include "binarytree.h"

int main() {

    //上图所示的二叉树先序遍历序列,其中用'#'表示结点无左子树或无右子树
    Element data[15] = {'A', 'B', 'D', '#', '#', 'E', '#', '#', 'C', 'F','#', '#', 'G', '#', '#'};
    Tree tree;
    treeNodeConstructor(tree, data);
    printf("深度优先遍历二叉树结果: ");
    depthFirstSearch(tree);
    printf("\n\n广度优先遍历二叉树结果: ");
    breadthFirstSearch(tree);
    return 0;

}