流行-Manifold【0】-维基百科中文版本解释




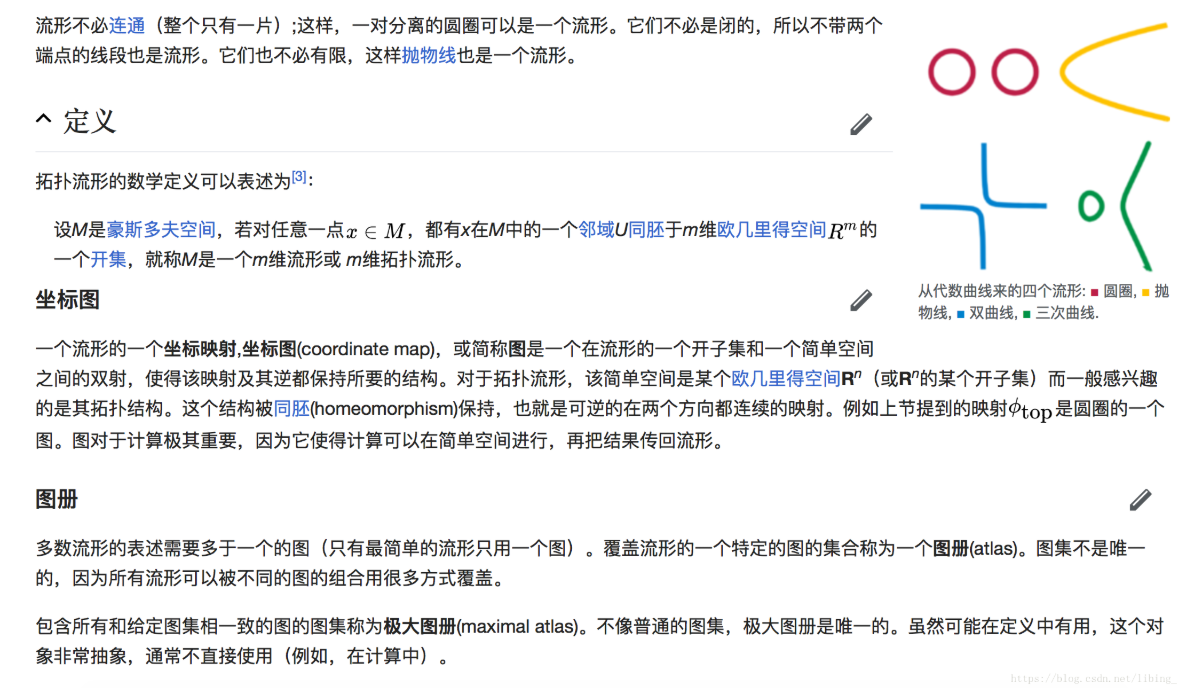











流行-Manifold【0】-维基百科中文版本解释的更多相关文章
- 小米2S TWRP 3.0.2-0 最新中文版本Recovery
注意:此版本为合并分区后的twrp 小米2S 合并分区教程:http://forum.xda-developers.com/mi-2/orig-development/flashtools-mifl ...
- Windows下基于python3使用word2vec训练中文维基百科语料(一)
在进行自然语言处理之前,首先需要一个语料,这里选择维基百科中文语料,由于维基百科是 .xml.bz2文件,所以要将其转换成.txt文件,下面就是相关步骤: 步骤一:下载维基百科中文语料 https:/ ...
- 中文维基百科分类提取(jwpl)--构建知识图谱数据获取
首先感谢 : 1.https://blog.csdn.net/qq_39023569/article/details/88556301 2.https://www.cnblogs.com/Cheris ...
- Windows下基于python3使用word2vec训练中文维基百科语料(二)
在上一篇对中文维基百科语料处理将其转换成.txt的文本文档的基础上,我们要将为文本转换成向量,首先都要对文本进行预处理 步骤四:由于得到的中文维基百科中有许多繁体字,所以我们现在就是将繁体字转换成简体 ...
- 使用word2vec对中文维基百科数据进行处理
一.下载中文维基百科数据https://dumps.wikimedia.org/zhwiki/并使用gensim中的wikicorpus解析提取xml中的内容 二.利用opencc繁体转简体 三.利用 ...
- 从0开始学爬虫8使用requests/pymysql和beautifulsoup4爬取维基百科词条链接并存入数据库
从0开始学爬虫8使用requests和beautifulsoup4爬取维基百科词条链接并存入数据库 Python使用requests和beautifulsoup4爬取维基百科词条链接并存入数据库 参考 ...
- 安装使用离线版本的维基百科(Wikipedia)
1 相关背景 平常大家在上网查询一些基本概念的时候常常会参考维基百科上面的资料,但是由于方校长研制的GFW(长城防火墙系统)强大的屏蔽功能,好多链接打开以后,不出意外会出现著名的“404NOT FOU ...
- 开源共享一个训练好的中文词向量(语料是维基百科的内容,大概1G多一点)
使用gensim的word2vec训练了一个词向量. 语料是1G多的维基百科,感觉词向量的质量还不错,共享出来,希望对大家有用. 下载地址是: http://pan.baidu.com/s/1boPm ...
- 维基百科 MediaWiki API 解析
使用开放的 API 做一个自己的小项目,是一个很好的学习方法.但好像开放的 API 选择并不多.这里给大家多一个选择,简单介绍一下维基百科使用的 MediaWiki API. 简介 先简单介绍几个容易 ...
随机推荐
- Python 元组、列表
Python中,最常用的数据结构就是序列了.序列有以下几种:元组,列表,字符串等.注:代码都是在IDE中编辑的,没有用交互式环境. 一.元组(tuple) 元组其实有点类似C++中的数组,即一旦指定了 ...
- UVa 12717 Fiasco (BFS模拟)
题意:给定一个错误代码,让你修改数据,使得它能够输出正确答案,错误代码是每次取最短的放入. 析:那么我们就可以模拟这个过程,然后修改每条边的权值,使得它能输出正确答案. 代码如下: #pragma c ...
- idea 快捷键以及包含字符串文件搜索
1.idea也有一个类似于eclipse的包含字符串文件搜索(特别实用) idea 里按快捷键:ctrl+H 2.下图是idea的快捷键汇总 3.debug调试 F5:跳入方法 F6:向下逐行调试 ...
- Reshapeing operations
Reshapeing operations Suppose we have the following tensor: t = torch.tensor([ [1,1,1,1], [2,2,2,2], ...
- Luogu P1073 最优贸易【最短路/建反图】 By cellur925
题目传送门 这么经典的题目,还是看了lyd的题解....唉难过. 一句话题意:在一张点有全都的图上找一条从1到n的路径,存在两个点p,q(p<q),使val[q]-val[p]最大. 给出的图是 ...
- 设置Google搜索在新的标签页打开
Google搜索的结果,默认情况下点击进入是在本标签页打开的,这样就很麻烦, 可以在搜索结果的页面中进行设置,让它在新的标签页显示 搜索结果设置->搜索设置->新的标签页打开
- Golang 在 Linux CentOS 6.5 服务器上实现 博客后台程序开机启动
在linux下想实现开机启动的方法很多,这里我采用了在/etc/rc.local里写shell指令的方式. 以下就以我的实际操作为例子讲述,很多地方需要看官自己调整信息哦! 1.在/etc/rc.lo ...
- nginx https反向代理tomcat
Context体现在server.xml中的Host里的<Context>元素,它由Context接口定义.每个<Context>元素代表了运行在虚拟主机上的单个Web应用. ...
- [SDOI2016]墙上的句子
题目描述 考古学家发现了一堵写有未知语言的白色墙壁,上面有一个n行m列的格子,其中有些格子内被填入了某个A至Z的大写字母,还有些格子是空白的. 一直横着或竖着的连续若干个字母会形成一个单词,且每一行的 ...
- poj 2195 Going Home (km算法)
题目链接: http://poj.org/problem?id=2195 解题思路: 把man和home都提取出来,然后算出每个man和home的距离算出来,然后建立匹配图,套用km算法的模板,求最小 ...
