图论-最短路径 floyd/dijkstra-Find the City With the Smallest Number of Neighbors at a Threshold Distance

2020-01-30 22:22:58

问题描述：

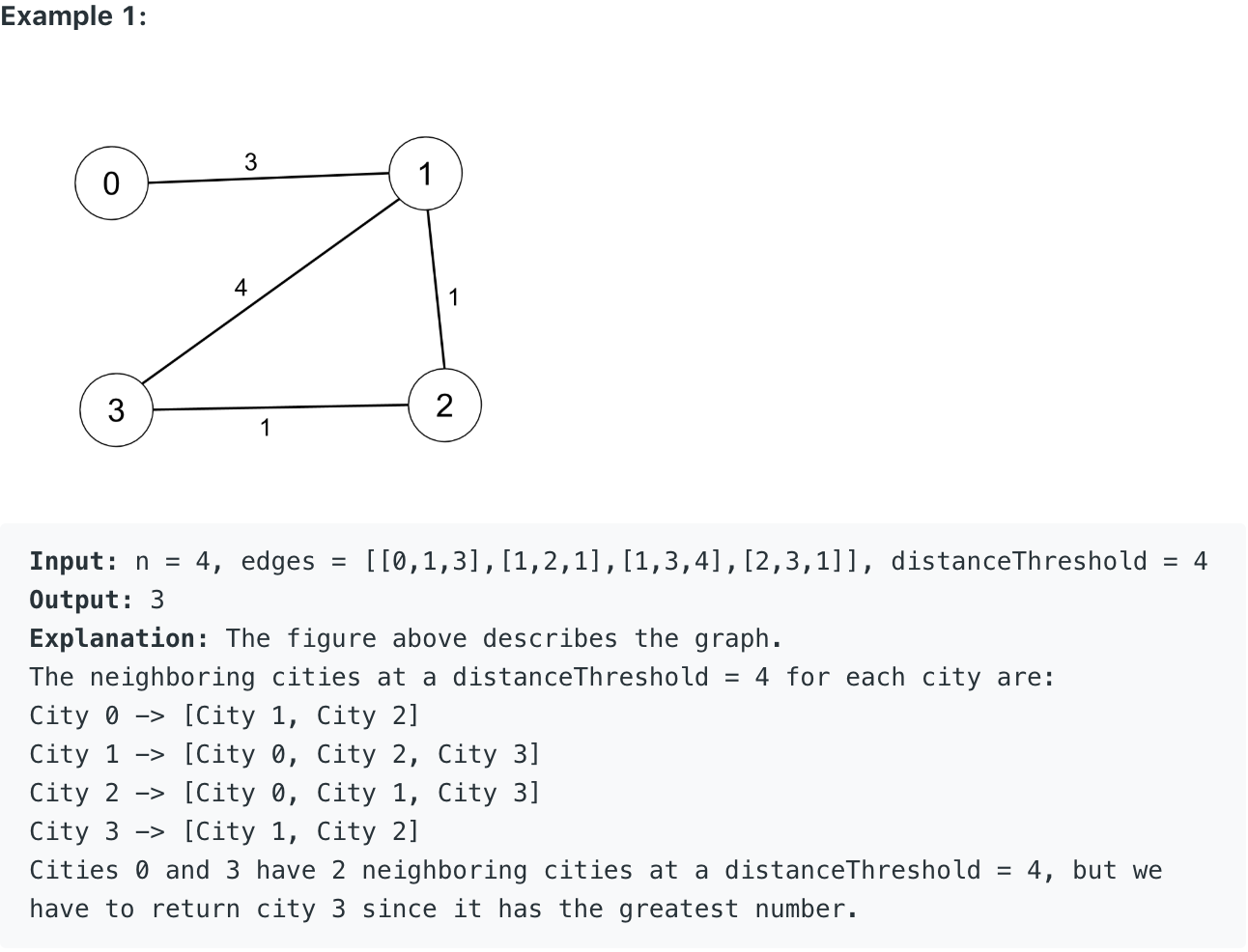
问题求解：

解法一：floyd

这个题目一看就是floyd解最合适，因为是要求多源最短路，floyd算法是最合适的，时间复杂度为O(n ^ 3)。

    int inf = (int)1e9;

    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        int[][] dp = new int[n][n];
        for (int i = 0; i < n; i++) Arrays.fill(dp[i], inf);
        for (int i = 0; i < n; i++) {
            dp[i][i] = 0;
        }
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            int d = edge[2];
            dp[u][v] = d;
            dp[v][u] = d;
        }
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (dp[i][j] > dp[i][k] + dp[k][j]) {
                        dp[i][j] = dp[i][k] + dp[k][j];
                    }
                }
            }
        }
        List<int[]> note = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                if (dp[i][j] <= distanceThreshold) cnt += 1;
            }
            note.add(new int[]{i, cnt});
        }
        Collections.sort(note, new Comparator<int[]>(){
            public int compare(int[] o1, int[] o2) {
                return o1[1] == o2[1] ? o2[0] - o1[0] : o1[1] - o2[1];
            }
        });
        return note.get(0)[0];
    }

解法二：dijkstra

使用邻接表 + 优先队列可以将单源最短路的时间复杂度降到O(ElogV)，所以整体的时间复杂度为O(VElogV)。

    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        List<int[]> record = new ArrayList<>();
        List<int[]>[] graph = new List[n];
        for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for (int[] edge : edges) {
            int from = edge[0];
            int to = edge[1];
            int w = edge[2];
            graph[from].add(new int[]{to, w});
            graph[to].add(new int[]{from, w});
        }
        for (int i = 0; i < n; i++) {
            int[] dist = new int[n];
            Arrays.fill(dist, (int)1e9);
            helper(graph, i, dist);
            int cnt = 0;
            for (int j = 0; j < n; j++) if (dist[j] <= distanceThreshold) cnt += 1;
            record.add(new int[]{i, cnt});
        }
        Collections.sort(record, (int[] o1, int[] o2) -> o1[1] == o2[1] ? o2[0] - o1[0] : o1[1] - o2[1]);
        return record.get(0)[0];
    }

    private void helper(List<int[]>[] graph, int node, int[] dist) {
        int n = graph.length;
        PriorityQueue<int[]> pq = new PriorityQueue<>((int[] o1, int[] o2) -> o1[1] - o2[1]);
        int[] used = new int[n];
        pq.add(new int[]{node, 0});
        while (!pq.isEmpty()) {
            int[] curr = pq.poll();
            int from = curr[0];
            int d = curr[1];
            if (used[from] == 1) continue;
            used[from] = 1;
            dist[from] = d;
            for (int[] next : graph[from]) {
                int to = next[0];
                int w = next[1];
                if (dist[to] > dist[from] + w) {
                    dist[to] = dist[from] + w;
                    pq.add(new int[]{to, dist[to]});
                }
            }
        }
    }