四元数--结合《real time rendering》中关于四元数部分
四元数产生于1843年,是复数的一个扩展,所以里面包含了一些复数的运算。直到1985年才在图形学中使用。
四元数的优势是,相对与矩阵和欧拉角,四元数更直观和方便。四元数还可以用作某些方向上的插值,而欧拉角可能并不能很好的完成。
四元数使用四个数字表示。通常,前三个和旋转的轴密切相关,最后一个和旋转的角度相关。以下是一些数学背景,对于后面的四元数的变化十分重要。
注意到四元数是复数的一个扩展,那么可以表示为:Û = (â, v), 其中 v 是一个实数,而 â 则是可以看成是虚部,且 â= i*qx + j*qy + k*qz 其中,i j k 都是虚部,他们的计算为
i2 = j2= k2 = -1 , jk = -kj=i , ik = -ki = j , ij = -ji = k ,因为â 含有三个部分,所以,一些向量的操作也是可以用在四元数的虚部上。
对于两个四元数相乘,如下图:
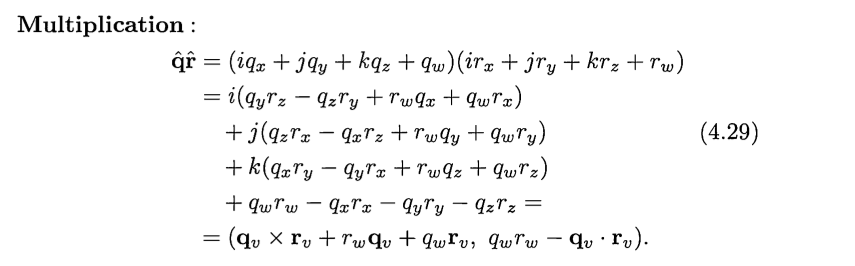
关于其他计算如下:
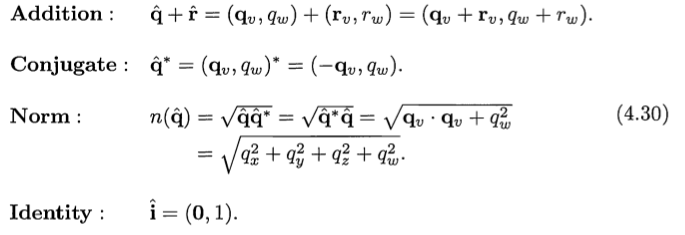
其中 conjugate 是共轭的意思。根据norm运算我们可以推出除法运算:
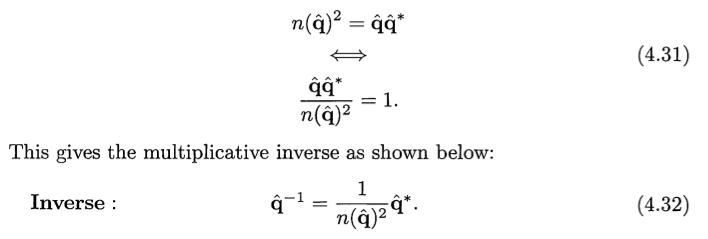
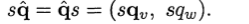
以及其他一些运算规则:

对于单位四元数,我们还可以用下面的方法进表示,这也是表达旋转变化比较直观的方式
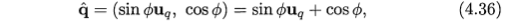
其计算过程如下,其中要求uq是单位向量:
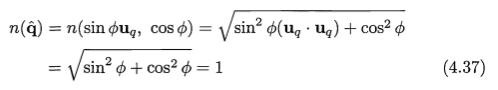
另一种表达方式如下,其可以解决log和平方运算:


对于单位四元数的直观理解如下图:

以上是四元数的基本知识背景。下面来介绍四元数表示的变化。
我们只使用四元数中的一个子集,单位四元数来进行各种旋转变化,十分简单和强大。变化方程为:

其q是一个单位四元数,其形式为公式4.36,而p则是一个四次其次的点或者向量,p的每个部分直接代替四元数的各个部分,形成一个新的四元数。注意到q是单位四元数,所以q-1 = q*。而且,单位四元数与实数相乘并不能改变四元数的作用效果,所以四元数q 和-q的作用效果一样的。那么在从矩阵转化到四元数的过程中,可能得到q也可能得到-q。公式4.40的直观理解就是上面的图。下面的公式代表两个四元数数对一个p进行变化。

四元数和矩阵的转化。因为在硬件上使用矩阵要比使用四元数计算的更快,所以可以在应用层面上使用四元数,但是在计算层面上使用矩阵。他们之间的转化为:
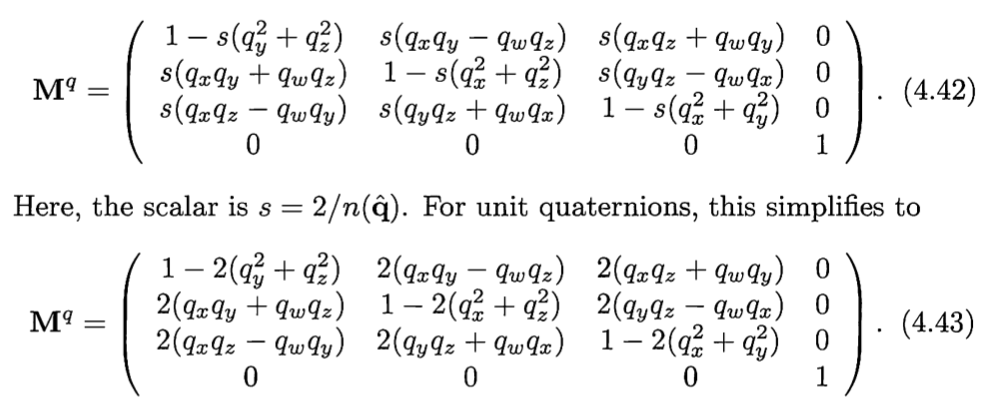
但是在应用层面上要使用四元数时,又要从矩阵转化成四元数。通过观察,可以看到以下等式
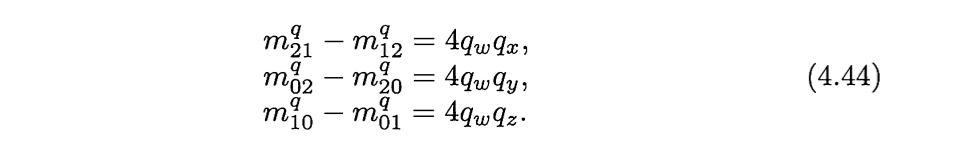
如果直到qw , qx , qy , qz中的任何一个,都可以计算出另外三个。通过观察可以知道如下等式:
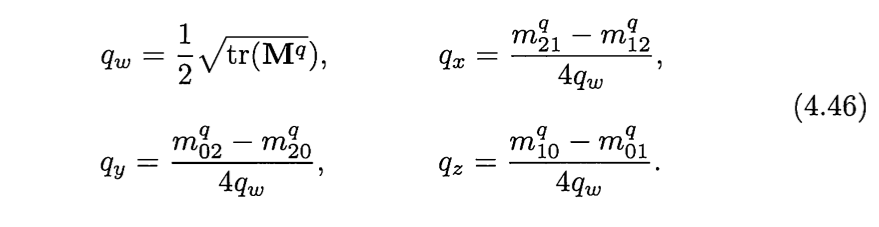
其中tr(Mq)的意思时矩阵的迹,也就是矩阵对角线的和。在计算过程中,我们知道应该尽量避免除以一个比较小的数字。所以4.46不一定时最好的算法。通过以下比较
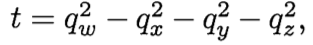
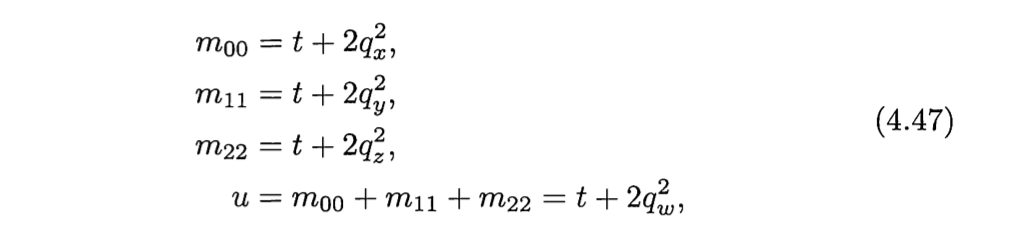
可知,通过比较矩阵的几个元素和u的大小就可以知道qx qy qz qw 的大小关系。如果qw 最大,那么直接使用4.46就可以。如果不是,那么可以使用如下方法,算出最大的那个元素值,然后决定使用4.44时那个元素作为分母。
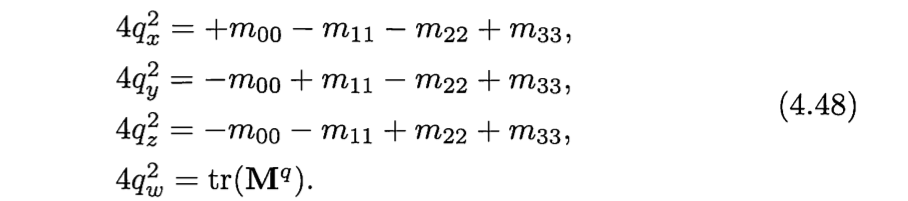
四元数--结合《real time rendering》中关于四元数部分的更多相关文章
- 【Unity编程】Unity中关于四元数的API详解
本文为博主原创文章,欢迎转载,请保留出处:http://blog.csdn.net/andrewfan Unity中关于四元数的API详解 Quaternion类 Quaternion(四元数)用于计 ...
- 四元数, Physx中的四元数
四元数的概念 & 如何使用四元数: 绕V轴旋转 f 角,对应的四元数: q = ( cos(f/2), Vx*sin(f/2), Vy*sin(f/2), Vz*sin(f/2) ) = c ...
- 视觉SLAM中的数学基础 第二篇 四元数
视觉SLAM中的数学基础 第二篇 四元数 什么是四元数 相比欧拉角,四元数(Quaternion)则是一种紧凑.易于迭代.又不会出现奇异值的表示方法.它在程序中广为使用,例如ROS和几个著名的SLAM ...
- 3D游戏与计算机图形学中的数学方法-四元数
说实话关于四元数这一节真的是不好懂,因为里面涉及到好多数学知识,单说推出来的公式就有很多.不怕大家笑话,对于四元数的学习我足足花了两天的时间,包括整理出这篇文章.在前面一章我写到了“变换”,这也是总结 ...
- Unity四元数小问题整理
1.Unity中,四元数不能保存超过360度的旋转,所以如此大范围的旋转不能直接两个四元数做插值(当你用0度和721度的四元数做插值,它只会转1度,而不会转两圈). 2.要把旋转设置成某个方向,用Lo ...
- 关于Unity四元数相乘先后顺序的问题
在unity中四元数和向量相乘在unity中可以变换旋转.四元数和四元数相乘类似矩阵与矩阵相乘的效果. 矩阵相乘的顺序不可互换,只有特殊条件矩阵才可互换.四元数相乘类似,今天就因为这个问题掉进坑里了, ...
- 3D数学基础:四元数与欧拉角之间的转换
在3D图形学中,最常用的旋转表示方法便是四元数和欧拉角,比起矩阵来具有节省存储空间和方便插值的优点.本文主要归纳了两种表达方式的转换,计算公式采用3D笛卡尔坐标系: 单位四元数可视化为三维矢量加上第四 ...
- [百度空间] [转] 四元数(Quaternions)
转:四元数(Quaternions) 好吧,我必须承认到目前为止我还没有完全理解四元数,我一度把四元数理解为轴.角表示的4维向量,也就在下午我才从和同事的争辩中理解了四元数不完全是角.轴这么简单,为此 ...
- Direct3D-3 四元数
其实本来这篇文章是打算接上篇的各种变化矩阵的推导了,想了想,还是先讲四元数吧.本人的文章并不会提到欧拉角,因为我自己没弄懂欧拉角的万向锁问题. 很多人学习数学时,会有这样一个疑惑,这东 ...
随机推荐
- Linux wget auto login and backup database
#!/bin/bash # 这是一份本来打算采用自动备份数据的代码,由于测试过程中出现了无法连接的问题,导致不能测试, # 于是最后放弃了这份代码的进一步的开发,但是记录还是有必要的 login_ur ...
- BZOJ4408: [Fjoi 2016]神秘数【主席树好题】
Description 一个可重复数字集合S的神秘数定义为最小的不能被S的子集的和表示的正整数.例如S={1,1,1,4,13}, 1 = 1 2 = 1+1 3 = 1+1+1 4 = 4 5 = ...
- ssh的时候提示No user exists for uid 501
原来是oh my zash升级导致的.关闭iterm2然后重新打开iterm2就可以了
- 扩展ScriptBundle,支持混淆加密javascript
一.需求: 在web开发中,经常会处理javascript的一些问题,其中就包括js的压缩,合并,发布版本以及混淆加密等等问题.在asp.net 开发中我们使用ScriptBundle已经可以解决ja ...
- Spark之 spark简介、生态圈详解
来源:http://www.cnblogs.com/shishanyuan/p/4700615.html 1.简介 1.1 Spark简介Spark是加州大学伯克利分校AMP实验室(Algorithm ...
- Phonegap 自定义插件
一.PhoneGap中js与Java之间相互调用分为同步和异步两种方式 1.同步:js调用Java类的方法,然后Java类的方法直接返回一个值给js端 2.异步:js调用Java类的方法,Java类的 ...
- zookeeper 运维
尽管zookeeper在编程上有很多的阱陷,API也非常的难用,但zookeeper服务本身可以说是很牢靠的了,所以在网上貌似关于运维的文章比较少. 但省心并不代表不会出麻烦,下面总结下zookeep ...
- CentOS 添加新硬件硬盘,扩展空间而无需重启虚拟机
运行如下命令,通过重新扫描 SCSI (注:Small Computer System Interface 小型计算机系统接口)总线并添加 SCSI 设备,系统就可以扩展操作系统的物理卷磁盘空间,而且 ...
- jQuery操作table tr td
1.鼠标移动行变色 $("#tab tr").hover(function(){ $(this).children("td").addClass("h ...
- React基本实例
学习React不是一蹴而就的事情,入门似乎也没那么简单.但一切都是值得的. 今天给大家带来一个详细的React的实例,实例并不难,但对于初学者而言,足够认清React的思考和编写过程.认真完成这个实例 ...
