做的那么多都是一些比较怎么说呢，都是在数网格一类的题目之中，这些题目有些有点固定的套路，而一些需要状态压缩的题目呢，则么是真正对状态转移的考验。

这道题呢，被彻底打脸了，以后一定要任性一点一道题做不出来就要坚持啃，不管你干什么，先a了再说。

但这道题我是真的伤，拿头去写估计也想不出来最后的解法。

第一眼，这不是很简单的dp么？设f[i]表示第i个状态得到的最大价值那么这个状态就是由i这个状态的所有子集所构成。当然本人哪想的出来什么子集直接暴力枚举了。

复杂度2^n^2^n没错这就是复杂度。只能的30分。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cstdio>

#include<cstring>

#include<string>

#include<ctime>

#include<cstdlib>

#include<cmath>

#include<queue>

#include<deque>

#include<vector>

#include<set>

#include<bitset>

#include<cctype>

#include<utility>

#include<map>

#include<algorithm>

#include<stack>

using namespace std;

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int maxn=;

int n,state,t=;

int v[<<maxn];//v[i]表示第i个状态的价值

int f[<<maxn];//f[i]表示到达第i个状态的最优解

void dfs(int x,int sum,int now)

{

    if(now==x){f[x]=max(f[x],sum);return;}

    for(int i=;i<=x;i++)

    {

        if(now&i)continue;

        dfs(x,sum+v[i],now|i);

    }

}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();state=(<<n)-;

    for(int i=;i<=state;i++)v[i]=read();

    dfs(state,,);

    //for(int i=1;i<=state;i++)dfs(i,0,0);

    put(f[state]);

    return ;

}

然后也没心情听那所谓的数学课，觉得是在浪费时间，学长也不讲什么那还不如自己学。

所以干脆就一直想，然后一直没想到优化的方法，然后叫了个学长帮我看看，康神看一眼就秒a了。

真的是强，帮我找出代码中TLE的原因的是wydalao 他说我的dfs应该枚举子集，对哦。

这是康神打的递推枚举子集然后成功AC的代码，跑的挺快的。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cstdio>

#include<cstring>

#include<string>

#include<ctime>

#include<cstdlib>

#include<cmath>

#include<queue>

#include<deque>

#include<vector>

#include<set>

#include<bitset>

#include<cctype>

#include<utility>

#include<map>

#include<algorithm>

#include<stack>

using namespace std;

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int maxn=;

int n,state,t=;

struct node{

    int v;

    int num;

}e[<<maxn];

//v[i]表示第i个状态的价值

int f[<<maxn];//f[i]表示到达第i个状态的最优解

int count(int x){

    int res=;

    for(;x;x>>=){

        if(x&) res++;

    }

    return res;

}

bool cmp(node a,node b){

    return a.num<b.num;

}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();state=(<<n)-;

    for(int i=;i<=state;i++)f[i]=read(),e[i].v=i;

    for(int i=;i<=state;i++)e[i].num=count(i);

    sort(e+,e+state+,cmp);

    for(int i=;i<=state;i++){

        int s=e[i].v;

        for(int s1=s;s1!=;s1=s&(s1-)){

            int s2=s^s1;

            f[s]=max(f[s1]+f[s2],f[s]);

        }

    }

    //for(int i=1;i<=state;i++)dfs(i,0,0);

    put(f[state]);

    return ;

}

细节处理也很对。敬佩三尺，真强啊。然后我十分的不服。

自己学了一下下枚举当前状态的子集，怒打了一个记搜，也算是A了这道题，自己思考的程度很深了，这道题没白费。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cstdio>

#include<cstring>

#include<string>

#include<ctime>

#include<cstdlib>

#include<cmath>

#include<queue>

#include<deque>

#include<vector>

#include<set>

#include<bitset>

#include<cctype>

#include<utility>

#include<map>

#include<algorithm>

#include<stack>

using namespace std;

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int maxn=;

int n,state,t=;

int v[<<maxn];//v[i]表示第i个状态的价值

int f[<<maxn];//f[i]表示到达第i个状态的最优解

int dfs(int x)

{

    if(f[x]!=)return f[x];

    for(int i=x;i;i=(i-)&x)

    {

        if(i==x)continue;

        int s1=x^i;

        dfs(i);dfs(s1);

        f[x]=max(f[x],f[s1]+f[i]);

    }

    return f[x]=max(f[x],v[x]);

}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();state=(<<n)-;

    for(int i=;i<=state;i++)v[i]=read();

    dfs(state);

    put(f[state]);

    return ;

}

代码中记搜和一些状态初始值刚好形成嵌套关系，我也不知道自己则么写的把细节处理的这么好，自己还是可以的。

学长的枚举子集方法比较难一点这里不再赘述。放一下枚举子集的方法。

for(int i=x;i;i=(i-)&x)

{

   int s1^i;

}

i是当前集合的子集，s1是当前集合的补集。这样复杂度就大大降低了。

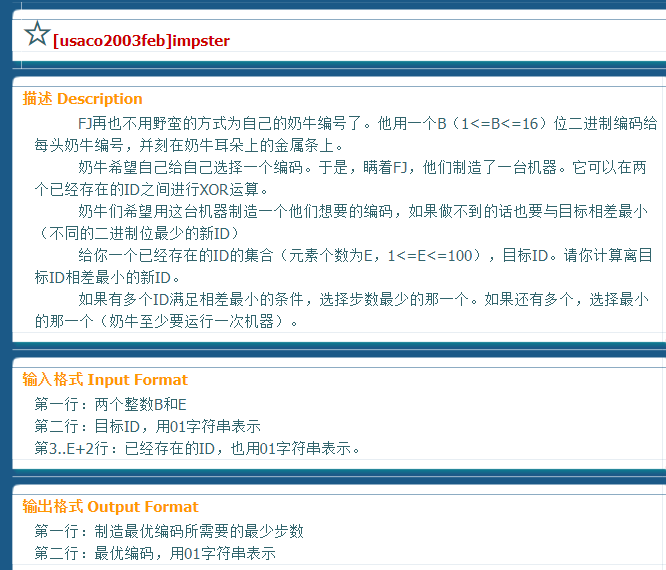
这道题的话也是很简单自己想的了状压dp，但是状态的设置和转移打了几个h都整不好，最后是qydalao教的，但是我不认同他的状态转移，但是a了就是事实。

//#include<bits/stdc++.h>

#include<iomanip>

#include<iostream>

#include<cstdio>

#include<cmath>

#include<ctime>

#include<cstdlib>

#include<cstring>

#include<string>

#include<set>

#include<bitset>

#include<queue>

#include<deque>

#include<stack>

#include<cctype>

#include<utility>

#include<algorithm>

#include<map>

#include<vector>

#define INF 214748364

using namespace std;

inline long long read()

{

    long long x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(long long x)

{

    x<?x=-x,putchar('-'):;

    long long num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    return;

}

const int MAXN=;

int n,m;

int f[<<];//f[i]表示第i个编码形成所需要的最小次数。

char a[][],an[];

int b[],cnt=,ans,maxx=,sum=,c[],t=;

int p[]={,,,,,,,,,,,,,,,,};

int contrast(int x,int y)

{

    int xx=;

    while()

    {

        if(x==&&y==)break;

        if((x&)!=(y&))xx++;

        x=x>>;y=y>>;

    }

    return xx;

}

int main()

{

    //freopen("1.in","r",stdin);

    m=read();n=read();

    scanf("%s",an+);

    for(int i=;i<=n;i++)scanf("%s",a[i]+);

    for(int i=m,j=;i>=;i--,j++)cnt+=an[i]==''?p[j]:;

    for(int i=;i<=(<<m);i++)f[i]=INF;

    for(int i=;i<=n;i++)

    {

        for(int j=m,t=;j>=;j--,t++)

        {

            b[i]+=a[i][j]==''?p[t]:;

        }

    }

    for(int i=;i<=n;i++)

    {

        for(int j=;j<=n;j++)

        {

            f[b[i]^b[j]]=min(f[b[i]^b[j]],);

        }

        f[b[i]]=;

    }

    for(int i=;i<=n;i++)

        for(int j=;j<(<<m);j++)

        {

            if(f[j]>)continue;

            f[j^b[i]]=min(f[j^b[i]],f[j]+);

        }

    for(int i=(<<m)-;i>=;i--)

    {

        if(f[i]!=INF)

        {

            int u=contrast(cnt,i);

            if(u==maxx){if(f[i]<sum)sum=f[i],ans=i;if(f[i]==sum)ans=min(ans,i);}

            if(u<maxx){maxx=u;sum=f[i];ans=i;}

        }

    }

    put(sum);puts("");

    while(ans)

    {

        if(ans&)c[++t]=;

        else c[++t]=;

        ans=ans>>;

    }

    if(t<m)t+=m-t;

    for(int i=t;i>=;i--)put(c[i]);

    return ;

}

关键是状态转移之处，最后的细节处理当然是简单的了。

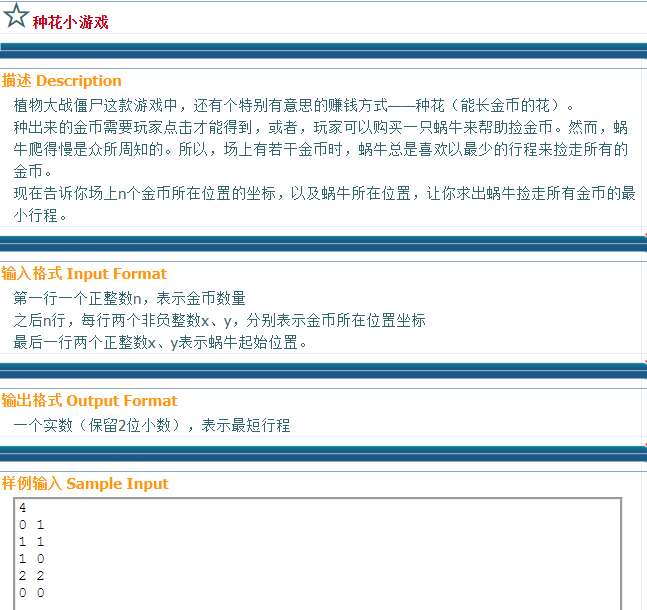
这道题是本人自己亲自相出来的思路，那天可能太聪明了，导致推出了正解，看着数据范围是状压。

也可以是状压，但是不免的是随机化搜索什么的，模拟退火好像也可以A了这道题。

但是本人亲自相出的思路那肯定是不一样的。对思维的真实锻炼。

大体思路就是设f[i][j]表示第i个状态到达了第j个节点所需费用的最小值。

那么这样的话考虑填表法得出，枚举当前状态到达了哪个节点，由哪个节点到达这个节点的一堆状态的转移可以得出最优解。

自己的思路，AC了就是很爽呢。

//#include<bits/stdc++.h>

#include<iomanip>

#include<utility>

#include<cctype>

#include<vector>

#include<deque>

#include<map>

#include<stack>

#include<queue>

#include<bitset>

#include<set>

#include<cstdlib>

#include<algorithm>

#include<iostream>

#include<cstdio>

#include<ctime>

#include<cmath>

#include<cstring>

#include<string>

#define INF 214748364.5

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?x=-x,putchar('-'):;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(num--);

    putchar('\n');return;

}

const int MAXN=;

int n,s1,s2,w;

double ans=INF,a[MAXN][MAXN];

int x[MAXN],y[MAXN];

int p[]={,,,,,,,,,,,,,,,,,};

double f[<<][];//f[i][j]表示达到第i个状态时所在的节点那么答案就是MIN{f[(1<<n)-1][j]};

int b[MAXN],t=;

double distance(int u1,int u2,int x1,int x2)

{

    return sqrt(((u1-x1)*(u1-x1)*1.0+(u2-x2)*(u2-x2)*1.0)*1.0);

}

void getstate(int x)

{

    int cnt=;

    while(x)

    {

        if(x&)b[++t]=cnt;

        x=x>>;cnt++;

    }

}

double min(double x,double y){return x<y?x:y;}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();

    for(int i=;i<=n;i++){x[i]=read();y[i]=read();}

    x[]=read();y[]=read();

    for(int i=;i<=(<<n);i++)for(int j=;j<=n;j++)f[i][j]=INF;

    f[][]=;

    for(int i=;i<=n;i++)

        for(int j=;j<=n;j++)

            a[i][j]=distance(x[i],y[i],x[j],y[j]);

    for(int i=;i<(<<n);i++)

    {

        t=;

        getstate(i);

        for(int j=;j<=t;j++)

            for(int k=;k<=t;k++)

            {

                if(b[j]!=b[k])f[i][b[j]]=min(f[i][b[j]],f[i-p[b[j]]][b[k]]+a[b[k]][b[j]]);

            }

    }

    for(int i=;i<=n;i++)ans=min(ans,f[(<<n)-][i]);

    printf("%.2lf",ans);

    return ;

}

状压dp学的还行，自己dp的水平也在不断上涨呢，觉得自己越来越强了。

加油！

状压dp的另一种形式的更多相关文章

  1. 状压dp终极篇（状态转移的思想）

    状压dp是将每种状态都压缩成用一个二进制串,然后利用位运算进行操作的dp,而凡是dp都需要进行状态转移 对于简单的dp问题只需要一个二维数组dp[ i ][ j ]就能解决 具体操作为首先把状态压缩为 ...

  2. BZOJ 2734 [HNOI2012]集合选数 (状压DP、时间复杂度分析)

    题目链接 https://www.lydsy.com/JudgeOnline/problem.php?id=2734 题解 嗯早就想写的题,昨天因为某些不可告人的原因(大雾)把这题写了,今天再来写题解 ...

  3. 状态压缩动态规划 状压DP

    总述 状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式 很多棋盘问题都运用到了状压,同时,状压也很经常和BFS及DP连用,例题里会给出介绍 有了状态,DP就比 ...

  4. POJ 1185 炮兵阵地 【状压DP】

    <题目链接> 题目大意: 司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队.一个N*M的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示),也可能是平 ...

  5. 状压DP初探·总结

    2018过农历新年这几天,学了一下状态压缩动态规划,现在先总结一下.   状态压缩其实是一种并没有改变dp本质的优化方法,阶段还是要照分,状态还是老样子,决策依旧要做,转移方程还是得列,最优还是最优, ...

  6. 【状压DP】【UVA11795】 Mega Man's Mission

    传送门 Description 你要杀n个怪,每杀掉一个怪那个怪会掉落一种武器,这种武器可以杀死特定的怪.游戏初始你有一把武器,能杀死一些怪物.每次只能杀一只,求有多少种杀怪方法. Input 多组数 ...

  7. 【[APIO/CTSC2007]动物园】状压DP

    题目测评:https://www.luogu.org/problemnew/show/P3622 题目描述 新建的圆形动物园是亚太地区的骄傲.圆形动物园坐落于太平洋的一个小岛上,包含一大圈围栏,每个围 ...

  8. 【状压DP】OpenJ_POJ - C17K Lying Island

    https://vjudge.net/contest/171652#problem/K [题意] 小岛上有n个人,有些是好人(一定是真话),有些是坏人(可能是真话也可能是假话),现在要判断最多有多少好 ...

  9. 【ZJOI2017 Round1练习&BZOJ4774】D3T2 road（斯坦纳树，状压DP）

    题意: 对于边带权的无向图 G = (V, E),请选择一些边, 使得1<=i<=d,i号节点和 n − i + 1 号节点可以通过选中的边连通, 最小化选中的所有边的权值和. d< ...

随机推荐

  1. numpy数组(5)-二维数组的轴

    numpy的mean(),std()等方法是作用于整个numpy数组的,如果是二维数组的话,也是整个数组,包括所有行和列,但我们经常需要它仅作用于行或者列,而不是整个二维数组,这个时候,可以定义轴ax ...

  2. easy_install与pip 区别

    作为Python爱好者,如果不知道easy_install或者pip中的任何一个的话,那么......   easy_insall的作用和perl中的cpan,ruby中的gem类似,都提供了在线一键 ...

  3. Total Command 常用快捷键

    压缩和解压缩文件Alt + F5 压缩选定文件                                       Alt + F9      解压压缩文件Alt + Shift + F9   ...

  4. 24款最好的jQuery日期时间选择器插件

    如果你正在创建一个网络表单,有很多事情你需要在你的应用程序中使用.有时您需要特别的输入,从用户的日期和时间,如发票日期,生日,交货时间,或任何其他此类信息.如果你有这样的需要,可以极大地从动态的jQu ...

  5. 【30集iCore3_ADP出厂源代码(ARM部分)讲解视频】30-12底层驱动之液晶画点驱动

    视频简介:该视频介绍iCore3应用开发平台中液晶驱动的方法. 源视频包下载地址:链接:http://pan.baidu.com/s/1qXQoOQo 密码:gvgo 银杏科技优酷视频发布区:http ...

  6. [原]关于在Python和C#之间消息传递的问题

    问题的描述: 鉴于Python强大的网络功能和丰富的开源组件和C#开发Windows Form程序时优秀的框架,使用Python和C#混合编程可以有效的结合二者的长处,快速开发产品. 然而在这两者之间 ...

  7. Ogre2.1 Hlms与渲染流程

    在我前面三篇说明Ogre2.x的文章里,第一篇大致说了下Hlms,第二篇说了下和OpenGL结合比较紧的渲染,本文用来说下Hlms如何影响渲染流程中,因为有些概念已经在前面二文里说过了,本文就不再提, ...

  8. json 报错'xxx is not JSON serializable'的处理方法

    场景: 报错: 原因: json不能对np.int64或者np.float64等类型进行序列化,可以通过自定义serializer或者直接类型转换来解决. 解决方法: 显式的把 date 转换成 in ...

  9. 避免在构造函数中调用虚方法（Do not call overridable methods in constructors）

    CLR中说道,不要在构造函数中调用虚方法,原因是假如被实例化的类型重写了虚方法,就会执行派生类型对虚方法的实现.但在这个时候,尚未完成对继承层次结构中所有字段的初始化.所以,调用虚方法会导致不可预测的 ...

  10. centos7设置时间和时区

    1.安装ntp服务软件包:yum install ntp 2.将ntp设置为缺省启动:systemctl enable ntpd 3.修改启动参数,增加-g -x参数,允许ntp服务在系统时间误差较大 ...