luoguP1791 [国家集训队]人员雇佣

题意

考虑先将所有价值加上，之后用最小割求最小代价。

考虑每个点对\((i,j)\)，我们这样建边：

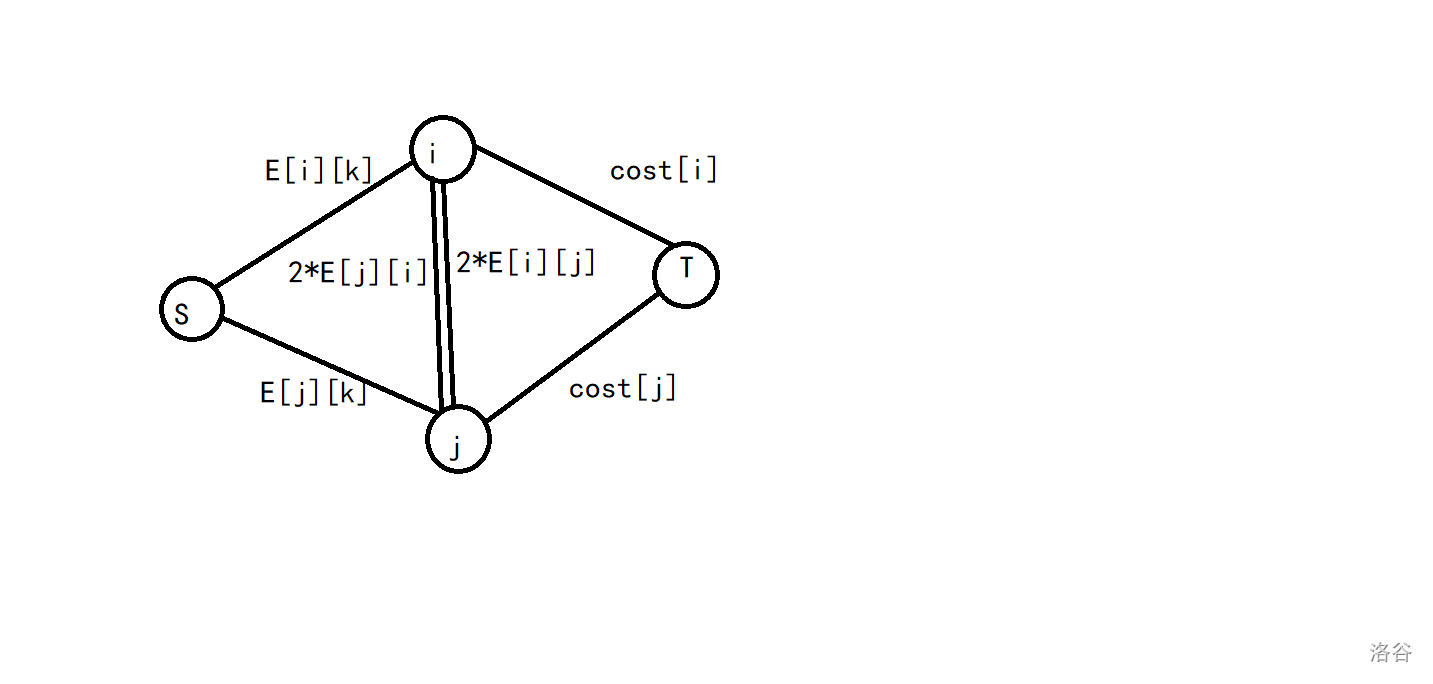
1.源点向每个点i连\(\sum\limits E_{i,j}\)容量的边。

2.每个点向汇点连雇佣代价容量的边。

3.对每个点对\((i,j)\)，从\(i\)向\(j\)连\(2*E_{i,j}\)容量的边。

考虑现在要割掉上图有什么割法：

1.割掉两个连向汇点的边，表示都选上了。

2.割掉两个连向源点的边，表示都不选。

3.割掉一条连向源点的，一条连向汇点的，一条连接两点的，表示一个选一个不选，那么我们要减去\(2*E_{i,j}\)，因为不仅之前加多了，这么选后还会再减\(E_{i,j}\)。

code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1010;
const int maxm=10010;
const ll inf=1e9;
int n,cnt=1,st,ed;
int head[maxn],cur[maxn],dep[maxn];
ll ans;
ll cost[maxn],sum[maxn];
ll a[maxn][maxn];
struct edge{int to,nxt;ll flow;}e[maxn*maxn<<1];
inline ll read()
{
	char c=getchar();ll res=0,f=1;
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')res=res*10+c-'0',c=getchar();
	return res*f;
}
inline void add(int u,int v,ll w)
{
	e[++cnt].nxt=head[u];
	head[u]=cnt;
	e[cnt].to=v;
	e[cnt].flow=w;
}
inline bool bfs()
{
	memset(dep,0,sizeof(dep));
	for(int i=0;i<=n+1;i++)cur[i]=head[i];
	queue<int>q;
	q.push(st);dep[st]=1;
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=e[i].nxt)
		{
			int y=e[i].to;
			if(dep[y]||e[i].flow<=0)continue;
			dep[y]=dep[x]+1;q.push(y);
		}
	}
	return dep[ed]>0;
}
ll dfs(int x,int goal,ll lim)
{
	if(x==goal||lim<=0)return lim;
	ll res=lim;
	for(int i=cur[x];i;i=e[i].nxt)
	{
		cur[x]=i;
		int y=e[i].to;
		if(e[i].flow<=0||dep[y]!=dep[x]+1)continue;
		ll tmp=dfs(y,goal,min(res,e[i].flow));
		if(tmp<=0)dep[y]=0;
		res-=tmp;
		e[i].flow-=tmp,e[i^1].flow+=tmp;
		if(res<=0)break;
	}
	return lim-res;
}
inline ll Dinic()
{
	ll res=0;
	while(bfs())res+=dfs(st,ed,inf);
	return res;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)cost[i]=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			a[i][j]=read(),ans+=a[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			sum[i]+=a[i][j];
	st=0,ed=n+1;
	for(int i=1;i<=n;i++)add(st,i,sum[i]),add(i,st,0);
	for(int i=1;i<=n;i++)add(i,ed,cost[i]),add(ed,i,0);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(i!=j&&a[i][j])add(i,j,2*a[i][j]),add(j,i,0);
	printf("%lld",ans-Dinic());
	return 0;
}