Luogu P2532 [AHOI2012]树屋阶梯 卡特兰数

接着压位OvO。。。

---

我不会告诉你答案就是卡特兰数。。。

为什么呢？

首先，$ans[0]=1,ans[1]=1,ans[2]=2$

对于$ans[3]$，我们可以发现他是这样来的：

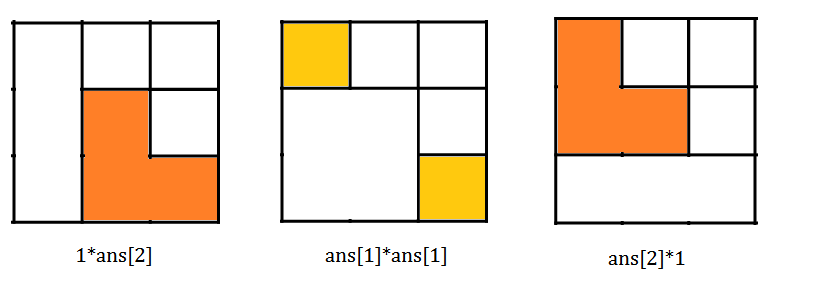
$ans[3]=\sum_{i=0}^{3-1}ans[i]*ans[n-i-1]$

而$ans[4]$呢？

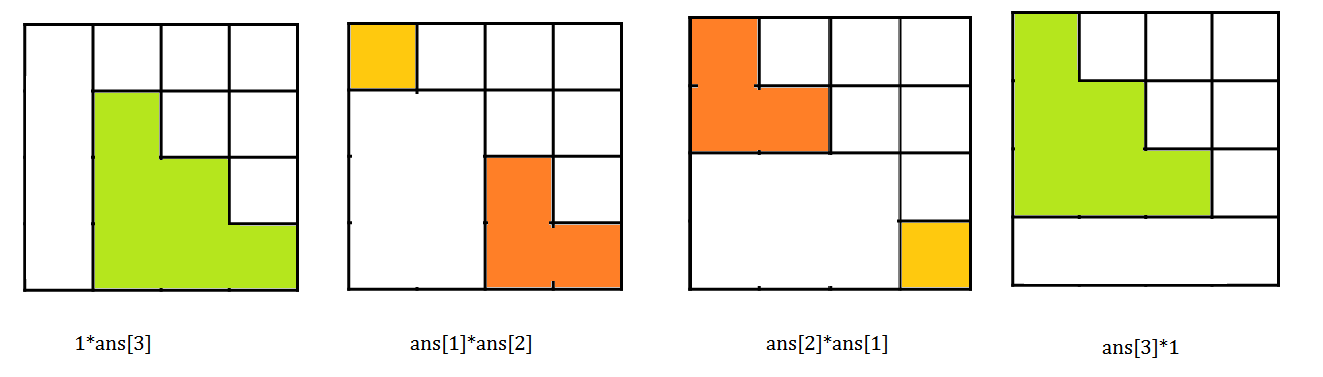
$ans[4]=\sum_{i=0}^{4-1}ans[i]*ans[n-i-1]$

woc。。。这不是卡特兰数嘛。。。

最后：要用高精qwq

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<vector>
#include<map>
#include<set>
#define ll long long
#define R register ll
static char RD[<<],*S=RD,*D=RD;
#define getchar() (S==D&&(D=(S=RD)+fread(RD,1,1<<15,stdin),S==D)?EOF:*S++)
const int W=,B=1E+,N=,L=;
using namespace std;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
struct Int {
    int sz; ll dat[];
    Int() {sz=; memset(dat,,sizeof(dat));}
    inline void init(int vl) {
        sz=; while(vl) ++sz,dat[sz]=vl%B,vl/=B;
    } inline void print() {
        printf("%lld",dat[sz]); for(R i=sz-;i;--i) printf("%09d",dat[i]);
    }
};
Int operator *(Int a,int b) {
    Int c; R lst=a.sz;
    for(R i=;i<=lst;++i) c.dat[i]=a.dat[i]*b;
    for(R i=;i<=lst;++i) c.dat[i+]+=c.dat[i]/B,c.dat[i]%=B;
    while(c.dat[lst+]) ++lst,c.dat[lst+]+=c.dat[lst]/B,c.dat[lst]%=B;
    c.sz=lst; return c;
}
Int ans;
int c[N],n;
inline void add(int x,int v) {
    for(R i=;i*i<=x;++i) while(x%i==) x/=i,c[i]+=v;
    if(x!=) c[x]+=v;
}
signed main() {
#ifdef JACK
    freopen("NOIPAK++.in","r",stdin);
#endif
    n=g(); for(R i=n+;i<=*n;++i) add(i,);
    for(R i=;i<=n;++i) add(i,-);
    ans.dat[]=ans.sz=; for(R i=;i<=*n;++i) while(c[i]) ans=ans*i,--c[i];
    ans.print();
} 

---

2019.06.05