[luogu P3648] [APIO2014]序列分割

[luogu P3648] [APIO2014]序列分割

题目描述

小H最近迷上了一个分隔序列的游戏。在这个游戏里，小H需要将一个长度为n的非负整数序列分割成k+1个非空的子序列。为了得到k+1个子序列，小H需要重复k次以下的步骤：

1.小H首先选择一个长度超过1的序列（一开始小H只有一个长度为n的序列——也就是一开始得到的整个序列）；

2.选择一个位置，并通过这个位置将这个序列分割成连续的两个非空的新序列。

每次进行上述步骤之后，小H将会得到一定的分数。这个分数为两个新序列中元素和的乘积。小H希望选择一种最佳的分割方式，使得k轮之后，小H的总得分最大。

输入输出格式

输入格式：

输入第一行包含两个整数n，k（k+1≤n）。

第二行包含n个非负整数a1，a2，...，an（0≤ai≤10^4），表示一开始小H得到的序列。

输出格式：

第一行包含一个整数，为小H可以得到的最大分数。

第二行输出 k个介于 1 到 n−1 之间的整数，表示为了使得总得分最大，你每次操作中分开两个块的位置。第 i 个整数 si​​ 表示第 i 次操作将在 s​i​​ 和 s​i+1​​ 之间把块分开。

如果有多种方案使得总得分最大，输出任意一种方案即可。

输入输出样例

输入样例#1：

7 3
4 1 3 4 0 2 3

输出样例#1：

108
1 3 5

说明

你可以通过下面这些操作获得 108108 分：

初始时你有一块 (4, 1, 3, 4, 0, 2, 3)(4,1,3,4,0,2,3)。在第 11 个元素后面分开，获得 4 \times (1 + 3 + 4 + 0 + 2 + 3) = 524×(1+3+4+0+2+3)=52 分。

你现在有两块 (4), (1, 3, 4, 0, 2, 3)(4),(1,3,4,0,2,3)。在第 33 个元素后面分开，获得 (1 + 3) \times (4 + 0 + 2 + 3) = 36(1+3)×(4+0+2+3)=36 分。

你现在有三块 (4), (1, 3), (4, 0, 2, 3)(4),(1,3),(4,0,2,3)。在第 55 个元素后面分开，获得 (4 + 0) \times (2 + 3) = 20(4+0)×(2+3)=20 分。

所以，经过这些操作后你可以获得四块 (4), (1, 3), (4, 0), (2, 3)(4),(1,3),(4,0),(2,3) 并获得 52 + 36 + 20 = 10852+36+20=108 分。

限制与约定

第一个子任务共 11 分，满足 1 \leq k < n \leq 101≤k<n≤10。

第二个子任务共 11 分，满足 1 \leq k < n \leq 501≤k<n≤50。

第三个子任务共 11 分，满足 1 \leq k < n \leq 2001≤k<n≤200。

第四个子任务共 17 分，满足 2 \leq n \leq 1000, 1 \leq k \leq \min{n - 1, 200}2≤n≤1000,1≤k≤minn−1,200。

第五个子任务共 21 分，满足 2 \leq n \leq 10000, 1 \leq k \leq \min{n - 1, 200}2≤n≤10000,1≤k≤minn−1,200。

第六个子任务共 29 分，满足 2 \leq n \leq 100000, 1 \leq k \leq \min{n - 1, 200}2≤n≤100000,1≤k≤minn−1,200。

斜率优化DP。还被卡了一会，应该是昨天没有完全理解。今天再努力理解了一下，发现有了新的认识。

显然，对于这一题，切割的顺序是无关的，只要确定断点就好了。

那么很容易就想到一个转移方程：

f[i]=max{f[j]+s[j](s[i]-s[j])}。

而我又get到了新的方法来解——>（正确姿势）

设k<j<i，对于i来说，取j的决策比k更优越，则满足f[j]+s[j](s[i]-s[j])>f[k]+s[k](s[i]-s[k])。

紫经过转化以后，变成了

-s[i]<((f[j]-s[j]^2)-(f[k]-s[k]^2))/(s[j]-s[k])

这很像一个斜率式，我们可以将-s[i]看做点(f[j]-s[j]^2,s[j])和点(f[k]-s[k]^2,s[k])之间连线的斜率，只有满足上式（大于-s[i]），j才比k更优越。

由于-s[i]是单调减的，所以对于i+1，i+2....显然都是取j比取k更优越，所以就可以不考虑k了，直接把它扔掉。

先脱离一下题目，为了方便考虑，我们设当k<j<i且slope(k,j)<-s[c]时，j比k更优。

那我们再考虑一下当k<j<i时，j什么时候是没用的。

设u，v两点间斜率为slope(u,v)，当前决策点为c，则

当slope(k,j)>slope(j,i)时，如果slope(k,j)>-s[c]，则k比j更优；如果slope(k,j)<-s[c]，则slope(j,i)<slope(k,j)<-s[c]，此时i比j更优。

所以在这种情况下无论何时，j都不会成为当前最优解。

然后我们便发现，如果我们用一个双端队列把这些可能会被用到的决策点依次存起来（按DP的顺序，也就是下标的从小到大或从大到小），

根据我们上面所提到的，把不需要的决策点去掉，对留下来的点中任意相邻三个点i、j、k，一定有s(k,j)<s(j,i)——也就是说，这个斜率是单调增的（或者对于有些题是单调减）。正如以下这个图片：

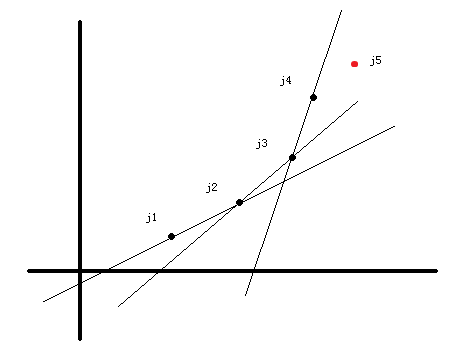
现在我们简单说一下如何维护这个单调队列，j1、j2、j3....是单调队列里当前正在维护的决策点，设我们的DP当前处理到了i。这些决策点还在单调队列里当且仅当这些点可能成为i、i+1、i+2...的最优决策点。

现在我们想要计算第i个点的f[i]，首先我们要找出单调队列里哪个点是i的最优决策点，我们从队首开始看起。

设队首的两个点为j1、j2，我们计算slope(j1,j2)，当slope(j1,j2)<−s[c])，j2比j1更优，我们把j1从单调队列中pop出来，以后也用不到了，然后再对slope(j2,j3)进行比较；

当slope(j1,j2)>−s[c]，j1比j2更优，且因为队列的单调性，slope(j2,j3)>slope(j1,j2)>−s[c]，也就是说j1优于j2优于j3...，则j1是对于当前点i最优的一个决策。

然后有了决策点，我们就可以计算出f[i]。现在我们来考虑将一个点添加到单调队列中去。

假设我们要添加的点为j5（如上图中红点），设队尾的两个点为j3、j4。

我们比较slope(j3,j4)与slope(j4,j5)，若slope(j3,j4)>slope(j4,j5)，则j4永远不可能是最优决策点，把j4，也就是队尾的点弹出，再依次比较；

若slope(j3,j4)<slope(j4,j5)满足斜率单调增的单调性，把j5，也就是DP到的当前节点插入到队尾。

然后再回到这题。这题的条件是当k<j<i时，slope(k,j)>-s[i]，j比k更优。那么刚好与上面相反，我们需要维护的是一个上凸包，即斜率越来越小。

还有，由于空间限制，这一题需要滚动数组，所以会有一些细节需要注意。

（Hint:部分摘自：http://www.cnblogs.com/akhpl/p/6715148.html，大力推荐）

code：（话说我的斜率DP写法很少人写啊。。。所以难查错）

 %:pragma GCC optimize()
 #include<bits/stdc++.h>
 #define sqr(x) ((x)*(x))
 #define LL long long
 using namespace std;
 ;
 const double inf=1e18;
 ],r[],roa[][N];
 LL s[N],f[][N];
 struct point {
     LL x,y; int i;
     point() {}
     point(LL _x,LL _y,int _i):x(_x),y(_y),i(_i) {}
 }st[][N];
 int read() {
     ,f=; char ch=getchar();
     :,ch=getchar();
     +ch-',ch=getchar();
     return x*f;
 }
 double slope(point u,point v) {
     return u.x==v.x?(u.y<v.y?inf:-inf):1.0*(v.y-u.y)/(v.x-u.x);
 }
 LL get(int y,int x,int i,LL k) {
     ])>1.0*k) l[i]++;
     roa[y][x]=st[i][l[i]].i;
     return st[i][l[i]].y-k*st[i][l[i]].x;
 }
 void insert(int i,point cur) {
     ],st[i][r[i]])<slope(st[i][r[i]-],cur)) r[i]--;
     st[i][++r[i]]=cur;
 }
 int main() {
     n=read(),k=read(),s[]=;
     ; i<=n; i++) s[i]=s[i-]+read();
     ,now,pre; j<=k; j++) {
         now=j&,pre=-now,l[pre]=,r[pre]=,st[++r[pre]][pre]=point(,,);
         ; i<=n; i++) {
             f[now][i]=get(j,i,pre,-s[i]);
             insert(pre,point(s[i],f[pre][i]-s[i]*s[i],i));
         }
     }
     printf(][n]);
     ; j--) i=roa[j][i],printf("%d ",i);
     ;
 }