一本通1609【例 4】Cats Transport

1609：【例 4】Cats Transport

时间限制: 1000 ms         内存限制: 524288 KB

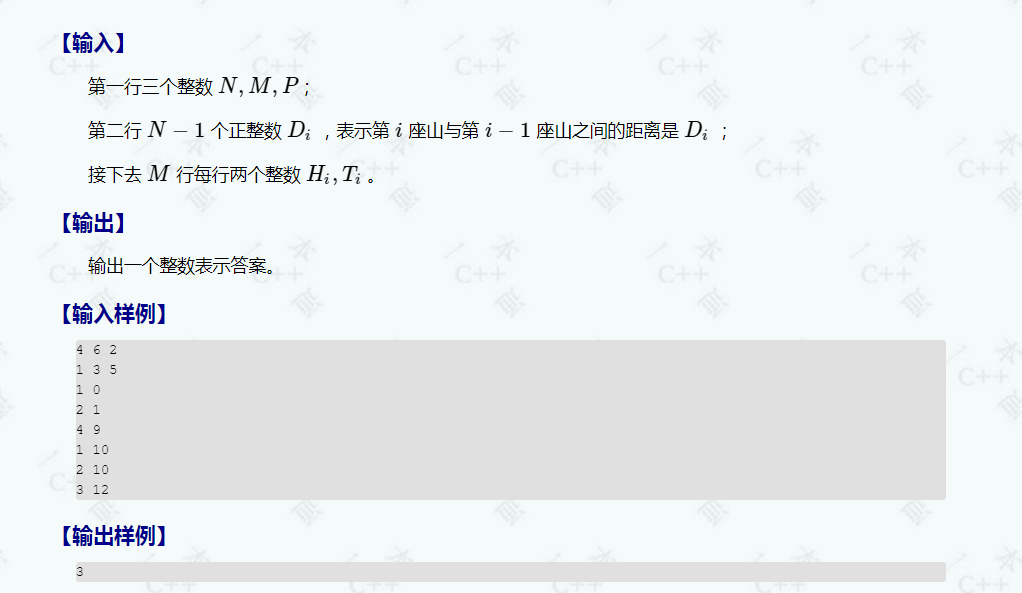
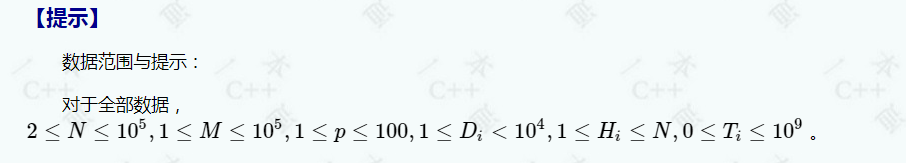
sol：非常偷懒的截图了事

注意：只能猫等人，不能人等猫

对于每只猫，我们可以得到一个数字 Cost[i] 表示Dis[H[i]]-T[i]，表示在Cost[i]时刻出发刚好不用等（如果出发时间小于Cost[i]，就会错过，反之则需要等待）

显然Cost需要排序

那么每个饲养员一定是掌管一段连续的Cost，直接dp是p*m²的，所以用斜率优化，非常套路

推出若 k<l<j

如果(dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k])<=(l-k)*Cost[j] 成立时 l 比 k 优

#include <bits/stdc++.h>
using namespace std;
typedef int ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+''); return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=,B=;
int n,m,P;
int Dis[N];
int H[N],T[N],Cost[N],Qzh[N];
int dp[N][B];
int main()
{
    int i,j,k;
    R(n); R(m); R(P);
    for(i=;i<=n;i++)
    {
        Dis[i]=Dis[i-]+read();
    }
    for(i=;i<=m;i++)
    {
        R(H[i]); R(T[i]); Cost[i]=T[i]-Dis[H[i]];
    }
    sort(Cost+,Cost+m+);
    for(i=;i<=m;i++)
    {
        Qzh[i]=Qzh[i-]+Cost[i];
    }
    memset(dp,,sizeof dp);
    dp[][]=;
    for(i=;i<=m;i++)
    {
        for(j=;j<=P;j++)
        {
            for(k=;k<i;k++)
            {
                dp[i][j]=min(dp[i][j],dp[k][j-]+Cost[i]*(i-k)-(Qzh[i]-Qzh[k]));
            }
        }
    }
    Wl(dp[m][P]);
    return ;
}

暴力代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+''); return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=,B=;
int n,m,P;
ll Dis[N];
ll H[N],T[N],Cost[N],Qzh[N];
ll dp[N],dp_Last[N];
int Que[N];
inline bool Panduan(int k,int l,int j) //k<l<j
{
    ll S1=(dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k]);
    ll S2=(l-k)*Cost[j];
    return (S1<=S2)?():;
}
inline bool Panduan_Rev(int k,int l,int j) //k<l<j
{
    ll S1=((dp_Last[l]+Qzh[l])-(dp_Last[k]+Qzh[k]))*(j-l);
    ll S2=((dp_Last[j]+Qzh[j])-(dp_Last[l]+Qzh[l]))*(l-k);
    return (S1>=S2)?():();
}
int main()
{
    int i,j,k;
    R(n); R(m); R(P);
    for(i=;i<=n;i++)
    {
        Dis[i]=Dis[i-]+read();
    }
    for(i=;i<=m;i++)
    {
        R(H[i]); R(T[i]); Cost[i]=T[i]-Dis[H[i]];
    }
    sort(Cost+,Cost+m+);
    for(i=;i<=m;i++)
    {
        Qzh[i]=Qzh[i-]+Cost[i];
        dp[i]=Cost[i]*i-Qzh[i];
    }
    for(i=;i<=P;i++)
    {
        memmove(dp_Last,dp,sizeof dp);
        int Head=,Tail=; Que[]=;
        for(j=;j<=m;j++)
        {
            while(Head<Tail&&Panduan(Que[Head],Que[Head+],j)) Head++;
            int Pos=Que[Head];
            dp[j]=dp_Last[Pos]+Cost[j]*(j-Pos)-(Qzh[j]-Qzh[Pos]);
            while(Head<Tail&&Panduan_Rev(Que[Tail-],Que[Tail],j)) Tail--;
            Que[++Tail]=j;
        }
    }
    Wl(dp[m]);
    return ;
}
/*
input
4 6 2
1 3 5
1 0
2 1
4 9
1 10
2 10
3 12
output
3
*/

斜率优化