51nod1298圆与三角形——（二分法）

1298 圆与三角形 

题目来源： HackerRank

基准时间限制：1 秒 空间限制：131072 KB 分值: 0 难度：基础题

 收藏

 关注

给出圆的圆心和半径，以及三角形的三个顶点，问圆同三角形是否相交。相交输出"Yes"，否则输出"No"。（三角形的面积大于0）。

 

Input

第1行：一个数T，表示输入的测试数量(1 <= T <= 10000)，之后每4行用来描述一组测试数据。
4-1：三个数，前两个数为圆心的坐标xc, yc，第3个数为圆的半径R。(-3000 <= xc, yc <= 3000, 1 <= R <= 3000）
4-2：2个数，三角形第1个点的坐标。
4-3：2个数，三角形第2个点的坐标。
4-4：2个数，三角形第3个点的坐标。(-3000 <= xi, yi <= 3000）

Output

共T行，对于每组输入数据，相交输出"Yes"，否则输出"No"。

Input示例

2
0 0 10
10 0
15 0
15 5
0 0 10
0 0
5 0
5 5

Output示例

Yes
No

题意：给出一个圆的圆心坐标以及圆的半径，三角形三个顶点的坐标，问你这个三角形和圆是否有交点。
思路：这一题刚看好像挺简单，在51nod上也是0分基础题，一开始觉得三个点都在圆外或都在圆内就不相交，否则就相交，但仔细一想却并没有那么简单。顶点是否在圆内只需要判断顶点到圆心的距离是否小于半径即可。这道题要分三种情况考虑：

第一种：三角形三个点到圆心的距离均小于半径（三个点都在圆内），如下图：



由上图可知，三个点在圆内可以确定没有相交。

第二种：有至少一个点在圆上或一部分在圆内一部分在圆外，如下图：

 

  

可以确定这一种情况一定相交；

第三种：三个顶点全在圆外，这种情况比较复杂，见下图：

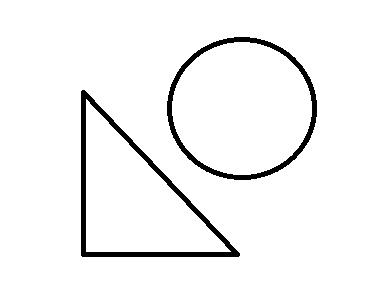
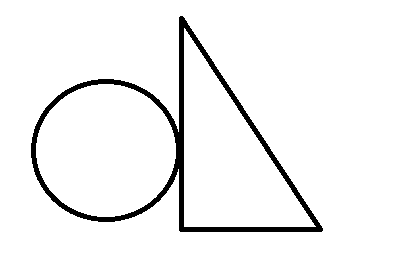
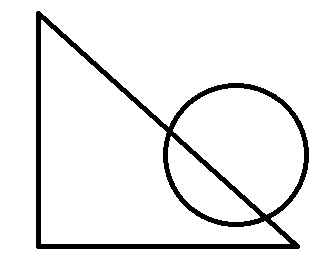
三个点都在外的主要分为这三种情况，那如何来进行判断呢？

这里可以用二分法来判断：分别用二分判断三条边，lowx，lowy，highx，highy表示边的两个端点，midx，midy表示边的中点，如果中点在圈内，那说明这条边肯定和圆有交点，因为边的端点都在圈外；如果中点在圈外，那就取线段其中的一半继续判断，取哪一半呢？我们可以想一下，如果相交，那在线段在圈内的那一段更靠近线段的哪一半，当然是端点更靠近圆心的那一半啊，就像上面的最后一张图，与左上角的端点相比，三角形右下角的端点更靠近圆心，所以相交的那一段更靠近右下角。正因为这样，我们二分时范围的改变就有了依据。二分的终止条件是什么？就是当中点与端点非常靠近时，这时可以等同于已经在端点处，无法再分了（貌似不是很严谨，但可以AC）。还有一点，当线段的两个端点的横坐标或纵坐标相等时，需要进行特判，因为横坐标相等时，中点的横坐标一直都等于端点横坐标的，这样二分可能会出现问题。下面看代码：

 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<stack>
 #include<queue>
 #define ll long long
 #define inf 0x3f3f3f3f
 using namespace std;

 int dir[][] = {{,},{,},{,}}; //用来表示三条边，分别以（1，2）（1，3） （2，3）为边的端点 

 int main()
 {
     int t;
     double xc,yc,r,x[],y[],farnode[];
     cin>>t;
     while(t--)
     {
         scanf("%lf%lf%lf",&xc,&yc,&r);//输入圆的坐标及半径
         int sum1 = ,sum2 = ;//sum1记录三角形在圆外的端点个数，sum2记录在圆内的端点个数
         for(int i=; i<=; ++i)
         {
             scanf("%lf%lf",&x[i],&y[i]);//输入三个端点
             farnode[i] = (x[i]-xc)*(x[i]-xc) + (y[i] - yc)*(y[i] - yc);//记录每个端点与圆心的距离
             if(farnode[i] > r*r) //到圆心的距离大于半径
                 sum1++;
             else if(farnode[i] < r*r) // 到圆心的距离小于半径
                 sum2++;
         }

         if(sum2 == ) //如果都在圆内
             printf("No\n");
         else if(sum1 == ) //如果都在圆外
         {
             int flag = ;
             double lowx,lowy,highx,highy;
             for(int i=; i<; ++i) //遍历三条边
             {
                 lowx = x[dir[i][]];
                 lowy = y[dir[i][]];
                 highx = x[dir[i][]];
                 highy = y[dir[i][]];

                 if(lowx == highx) //特判端点横坐标相等的情况
                 {
                     if(fabs(lowx-xc) <= r)
                     {
                         if((lowy >= yc && highy <= yc) || (lowy<= yc && highy>= yc))
                             flag = ;
                     }
                 }

                 else if(lowy == highy) //特判端点纵坐标相等的情况
                 {
                     if(fabs(lowy-yc) <= r)
                     {
                         if((lowx >=xc && highx <= xc)|| (lowx<= xc && highx>= xc))
                             flag = ;
                     }
                 }

                 else//否则二分判断
                 {
                     double midx,midy,lon,lonl,lonr;
                     midx = (lowx + highx)/;
                     midy = (lowy + highy)/;
                     while(midx - lowx > 0.1 || midx - lowx < -0.1) //当中点非常接近端点时结束循环
                     {
                         lon = (midx - xc)*(midx - xc) + (midy - yc)*(midy - yc);//求出中点在与圆心的距离
                         if(lon <= r*r) //如果在圆内则表示相交
                         {
                             flag = ;
                             break;
                         }
                         lonl = (lowx - xc)*(lowx - xc) + (lowy - yc)*(lowy - yc); // 计算两个端点到圆心的距离
                         lonr = (highx - xc)*(highx - xc) + (highy - yc)*(highy - yc);
                         if(lonl > lonr) //如果右端点靠近圆心，那就继续查找线段的右边一半
                         {
                             lowx = midx;
                             lowy = midy;
                         }
                         else if(lonl < lonr) //否则查找左边一半
                         {
                             highx = midx;
                             highy = midy;
                         }
                         else break;
                         midx = (lowx + highx)/; //继续取中点
                         midy = (lowy + highy)/;
                     }
                 }
                 if(flag) break;
             }
             if(flag) printf("Yes\n");
             else printf("No\n");
         }
         else
             printf("Yes\n");
     }
     return ;
 }

 /*
 3
 -7 3 1
 -8 -7
 -3 9
 -8 7
 */