2019ccpc秦皇岛/Gym102361 F Forest Program 仙人掌上dfs

题意：

某地沙漠化严重，沙漠里长了很多仙人掌，现在要让你删掉仙人掌的一些边让它的所有连通分量都是树，就完成了沙漠绿化（什么鬼逻辑？）让你计算删边的方案数。

仙人掌是一种特殊的图，它的每一条边只属于1或0条回路。

题解：

画几个仙人掌就能明白，仙人掌就是一棵树上的某些点长出了回路，可以把仙人掌分成若干个回路和不属于回路的边，要把仙人掌删成树不难，每个回路至少删掉一条边，即减掉一种所有回路边都不删的的方案，所有非回路边删或不删均可，假设非回路边有$a_0$个，第i个回路有$a_i$条边$(i=1,2....n)$，容易得出方案数是$2^{a_0}*\prod _{i=1}^{n} 2^{a_i}-1$

难点在于怎样找出仙人掌的所有回路，一种方法是dfs，记录边的深度，一旦从深度高的边dfs到了深度低的边，即找到了一个环，dfs过程中有如下几种情况：

1，dfs到了父亲，不用管，直接continue

2，dfs到了深度比自己浅的点，就是找到了环，环边数为两点深度之差+1，如下图从5到1

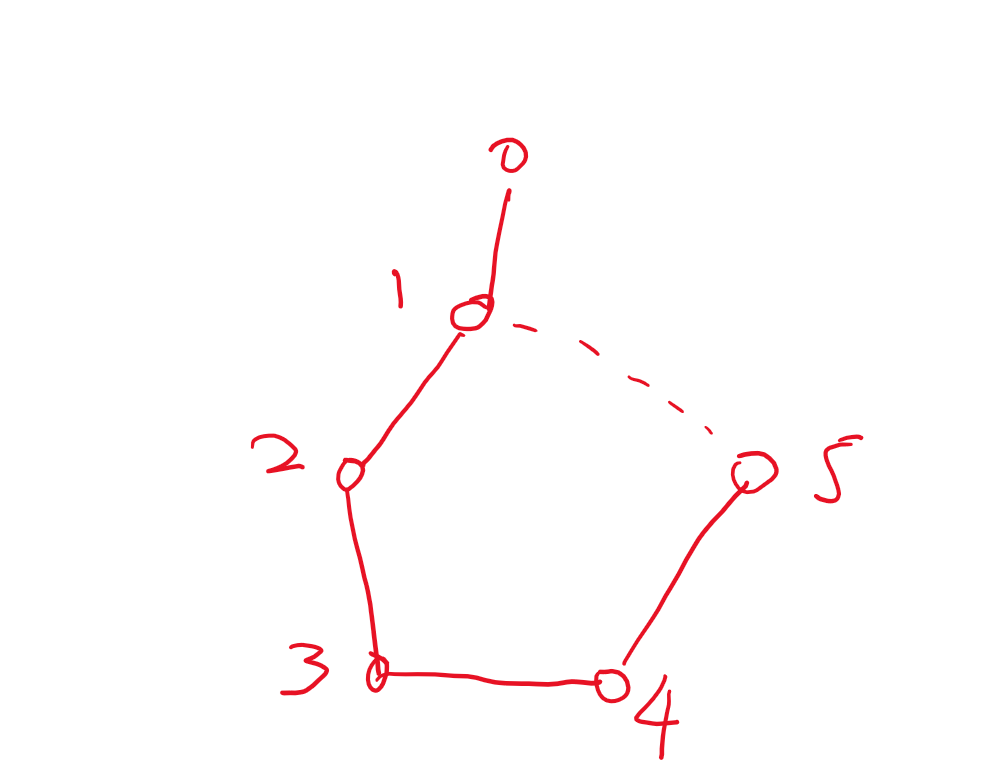
3，dfs到了 比自己深度深的点，则是访问到了统计过的环，也不管

4，dfs到了未标记深度的点，将此点深度记为父节点深度+1并从此点开始dfs

此题坑点在于图未必是连通图，需要从每一个未标记深度的点开始dfs

#include<iostream>
#include<vector>
#include<cstring>
#define MOD 998244353
#define LL long long
using namespace std;
LL qpow(LL base,int n){
    LL ans=;
    while(n){
        if(n&)ans=ans*base%MOD;
        base=base*base%MOD;
        n>>=;
    }
    return ans;
}
int vis[];
//0代表没访问过 1代表访问过 2代表访问过且已作为环找到过
int depth[];
vector<int> edge[];
vector<int> cnt;
void dfs(int u,int fa,int dpt){
    int l=edge[u].size();
    depth[u]=dpt;
    for(int i=;i<l;i++){
        int v=edge[u][i];
        if(v==fa || depth[v]>dpt)continue;
        //printf("u:%d %d v:%d %d\n",u,dpt,v,depth[v]);
        if(depth[v]>= && depth[v]<depth[u]){
            cnt.push_back(depth[u]-depth[v]+);
            //printf("Bingo%d\n",dpt-depth[v]+1);
            //depth[u]=dpt;
        }else{
            //depth[u]=dpt;
            //vis[u]=1;
            dfs(v,u,dpt+);
        }

    }
}
int main(){
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=;i<=m;i++){
        int a,b;
        scanf("%d %d",&a,&b);
        edge[a].push_back(b);
        edge[b].push_back(a);
    }
    memset(depth,-,sizeof depth);
//    dfs(1,-1,0);
    for(int i=;i<=n;i++){
        if(depth[i]==-)dfs(i,-,);
    }
    int sz=cnt.size();
    long long ans=;
    for(int i=;i<sz;i++){
        //printf("%d\n",cnt[i]);
        ans=ans*(qpow(,cnt[i])-)%MOD;
        m-=cnt[i];
    }
    ans=ans*qpow(,m)%MOD;
    printf("%lld\n",ans);
    return ;
}