机器学习-无监督机器学习-LDA线性判别分析-25

目录

• 1. Linear Discriminant Analysis 线性判别分析

1. Linear Discriminant Analysis 线性判别分析

经常被用于分类问题的降维技术，相比于PCA，LDA可以作为一种有监督的降维算法，降维的时候用到了y的真实值，有监督的降维。

在PCA中，算法没有考虑数据的标签（类别），只是把原数据映射到一些方差比较大的方向上而已。



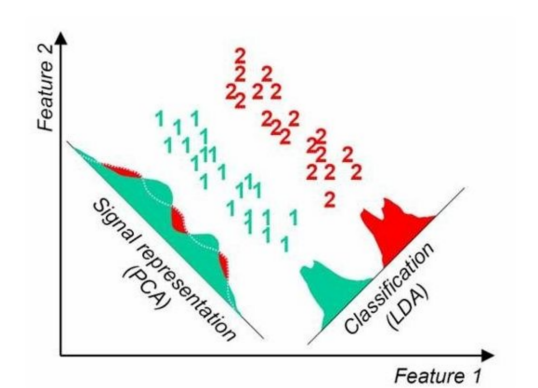
如下图所示，根据PCA算法，数据应该映射到方差最大的那个方向上，但是，两个不同类别的数据就会完全混合在一起，很难区分开。所以，使用PCA算法进行降维后再进行分类的效果会非常差；但是，如果使用LDA算，数据会反而映射到成90度的另外一个轴方向。

从一个简单的二分类问题出发，有C1， C2两个类别的样本



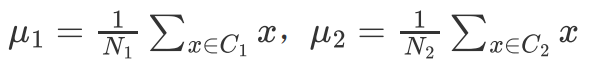
可以计算起均值也就是中心所在的位置。

希望投影之后两类之间的距离尽可能大，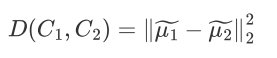

其中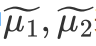

表示两类的中心在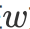

方向上的投影向量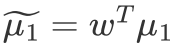



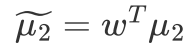
因此需要优化的问题为：



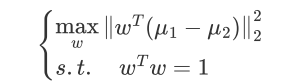
当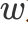

方向与

一致的时候，该距离达到最大值，

LDA的中心思想：最大化类间距离和最小化类内距离

数学表达：





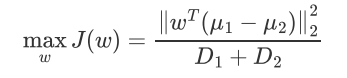
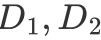
分别表示两类投影后的方差

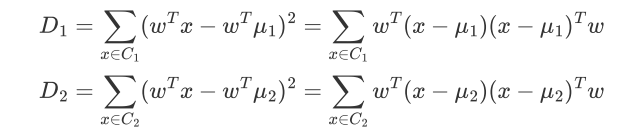
定义类间散度：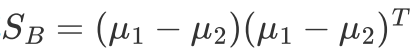

类内散度：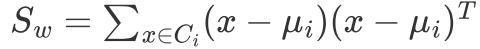

目标函数变成：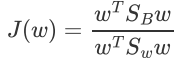

对w求偏导，并令导数等于零得到：



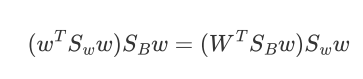
令：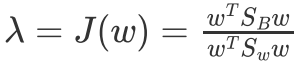

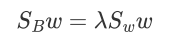
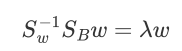
这个式子就很熟悉了，特征值与特征向量。



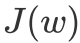
就对应了矩阵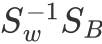

最大的特征值，而投影方向就是这个特征值对应的特征向量，这就是对于LDA给出我们的最优解。

LDA求解方法：

1 计算数据集中每个类别样本的均值向量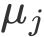

，及总体均值向量

2 计算类内散度矩阵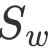

，全局散度矩阵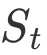

，并得到类间散度矩阵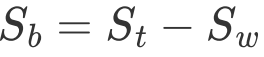

3 对矩阵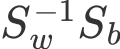

进行特征值分解，将特征值从大到小排列

4 取特征值前d大的对应的特征向量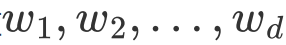

，通过以下映射将n维样本映射到d维

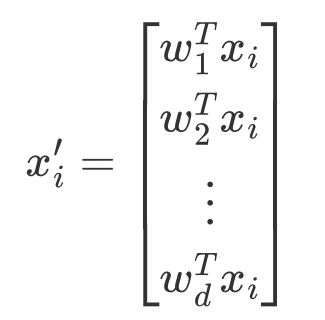
总结：

另外，在人脸识别领域中，PCA和LDA都会被频繁使用。基于PCA的人脸识别方法也称为特征脸（Eigenface）方法，该方法将人脸图像按行展开形成一个高维向量，对多个人脸特征的协方差矩阵做特征值分解，其中大特征值对应的特征向量具有与人脸相似的形状，故称为特征脸。人脸识别在降维后的空间上进行，由于其利用PCA进行降维，一般情况下保留的是最佳描述特征（主成分），而非分类特征。如果我们想要达到更好的脸识别效果，应该用LDA方法对数据集进行降维，使得不同人脸在投影后的特征具有一定区分性。