Normalization Methods

概
主要内容

Ioffe S. and Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning (ICML), 2015.

Ba J., Kiros J. and Hinton G. Layer normalization. In Advances in Neural Information Processing Systems (NIPS) 2016.

Ulyanov D., Vedaldi A. and Lempitsky V. Instance normalization: the missing ingredient for fast stylization.arXiv preprint arXiv:1607.08022, 2016.

Wu Y. and He K. Group normalization. In Proceedings of the European conference on computer vision (ECCV), 2018.

概

整理一下各种normalization方法.

主要内容

对于每一层, 可以简化的理解为:

\[h^l = f(Wh^{l-1} + b),
\]

其中\(h^{l}\)是前一层的输入, \(W, b\)分别为该层的权重和偏置, \(f\)是对应的激活函数.

但是仅按照这种方式搭建的网络训练不稳定还非常慢, 这也是为什么各种normalization方法被提出的初衷.

这些方法可以统一为:

\[h^{l} = f(g(Wh^{l-1} + b)),
\]

这里用\(g(\cdot)\)表示某种normalization方法.

为了方便起见, 另外令

\[x = Wh^{l-1} + b, \\
y = g(x).
\]

总的示意图如下(图片来自Group Normalization):

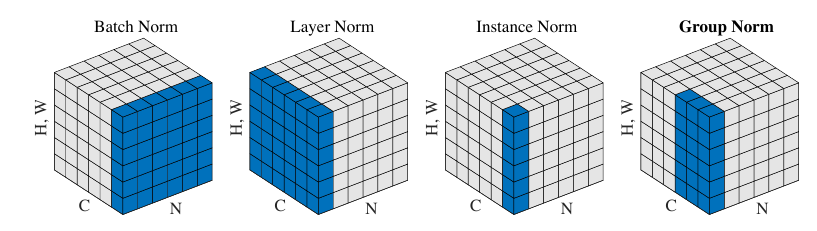
Batch Normalization

该normalization方法思想是最朴素的, 即每一次我们都recentering一下数据:

\[y = g(x) = \frac{x - \mu}{\sigma},
\]

这里\(\mu,\sigma\)分别表示\(x\)的均值和标准差.

但是上述的标准化存在均值和标准差的估计问题, 故在训练中我们取一个batch作为估计:

\[y = \frac{x - \hat{\mu}}{\hat{\sigma}}, \quad \hat{\mu}:= \frac{1}{n} \sum_{i=1}^n x^i, \hat{\sigma} := \sqrt{\frac{1}{n}\sum_i (x^i - \hat{\mu})^2}.
\]

其中\(x^i, i=1,2,\cdots, n\)为一个batch的数据.

在实际中, 为了安全和可扩展, 采取如下形式:

\[y = \frac{x - \hat{\mu}}{\sqrt{\hat{\sigma}^2+\epsilon}} \cdot \gamma + \beta,
\]

其中\(\gamma, \beta\)为weight 和 bias, \(\epsilon\)常取1e-5.

在训练中, 每次forward pass都会更新running_mean \(\mu\), running_var \(\sigma^2\):

\[\mu = (1 - m) \cdot \mu + m \cdot \hat{\mu} \\
\sigma^2 = (1 - m) \cdot \sigma^2 + m \cdot \hat{\sigma}^2.
\]

这里\(m\)是用于滑动平均的momentum, 这里采取这种形式是为了和Pytorch的实现保持一致, 其选择\(m=0.1\).

在evaluation中, 我们变使用\(\mu, \sigma^2\)来normalization:

\[y = \frac{x - \mu}{\sqrt{\sigma^2+\epsilon}} \cdot \gamma + \beta.
\]

注: 在处理\(dim=1\)(即向量数据)的时候, 均值和方差的计算就是普通的, 但是\(dim=2\)的时候, 比如常见的卷积mapping, 其结构为\(N \times C \times H \times W\), 则其均值方差是对于每一个通道计算的, 即\(\mu,\sigma \in \mathbb{R}^C\), 同理\(\gamma, \beta \in \mathbb{R}^C\).

Layer Normalization

显然, batch normalization的batch size 不能太小, 而layer normalization 可以处理这一点, 因为它是针对单个样本而言的.

其同样采取

\[y = \frac{x - \hat{\mu}}{\sqrt{\hat{\sigma}^2+\epsilon}} \cdot \gamma + \beta,
\]

的形式, 只是

\[\hat{\mu} := \frac{1}{H} \sum_{i}^H x_i,\: \hat{\sigma}:= \sqrt{\frac{1}{H}\sum_{i=1}^H (x_i - \hat{\mu})^2},
\]

这里\(x_i\)表示\(x\)的第\(i\)个分量, 特征维度为\(H\).

注: 在Pytorch的实现中, \(\gamma, \beta\)都是element-wise的, 即如果我们选取\(C \times H \times W\), 则\(\gamma, \beta \in \mathbb{R}^{C \times H \times W}\).

Instance Normalization

instance normalization 主要是用于消除图片之间的contrast而提出的:

\[y = \frac{x - \hat{\mu}}{\sqrt{\hat{\sigma}^2+\epsilon}} \cdot \gamma + \beta,
\]

注意, instance的normalization同样是基于单个样本而言的, 对于卷积层而言\(N \times C \times H \times W\):

\[\hat{\mu} := \frac{1}{HW}\sum_i \sum_j x_{ij}, \\
\hat{\sigma} := \sqrt{\frac{1}{HW}\sum_i \sum_j (x_{ij} - \hat{\mu})^2},
\]

显然\(\hat{\mu}, \hat{\sigma} \in \mathbb{R}^C\). 对于向量数据而言, 和layernorm其实是一致的.

注: instance normalization 通常没有放射变换(即舍弃\(\gamma, \beta\)).

Group Normalization

GN则是根据通道\(C\)分成\(G\)个group, 对每一个group沿着\(H, W\)方向估计:

\[\hat{\mu}_g := \frac{1}{(C / G) \cdot HW} \sum_{i=1}^H\sum_{j=1}^W\sum_{k=(g - 1)\cdot \frac{C}{G} + 1}^{g * \frac{C}{G}} x_{kij}, \\
\hat{\sigma}_g := \sqrt{\frac{1}{(C / G) \cdot HW} \sum_{i=1}^H\sum_{j=1}^W\sum_{k=(g - 1)\cdot \frac{C}{G} + 1}^{g * \frac{C}{G}} (x_{kij} - \hat{\mu}_g)^2}, \\
g = 1, 2, \cdots, G.
\]

注: 这里假设\(C\)能够整除\(G\).

注: 当\(G=C\)的时候, GN 就是 IN, \(G=1\)的时候, GN就是LN.