MT【200】一道自招的不等式

(2018武汉大学自招)设$x,y,z\ge0,xy+yz+zx=1$证明:$\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\ge \dfrac{5}{2}$

证明:
\begin{align*}
\textbf{原式} & \iff 2\sum{(y+z)(z+x)}-5\prod(x+y)\ge0\\
& \iff 2\sum{z^2+(x+y)z+xy}-5\left((x+y+z)(xy+yz+zx)-xyz\right)\ge0\\
& \iff 2(x+y+z)^2+2-5(x+y+z)+5xyz\ge0
\end{align*}
记$a=x+y+z,b=xy+yz+zx,c=xyz$则只需证明:$2a^2-5a+5c+2\ge0$
若$a>2$则$2a^2-5a+5c+2\ge2a^2-5a+2=(2a-1)(a-2)\ge0$成立
若$a\le2$则由舒尔不等式:
$\sum{x(x-y)(x-z)=(\sum x)^3-4\sum{x}\sum{xy}+9xyz=a^3-4ab+9c=a^3-4a+9c\ge0}$ 得
$c\ge\dfrac{-a^3+4a}{9}$
故$2a^2-5a+5c+2\ge\dfrac{-5a^3+18a^2-25a+18}{9}\ge0$(由单调递减易得)当$(x,y,z)=(1,1,0)$时取到等号.

事实上还有如下天书上的证明:

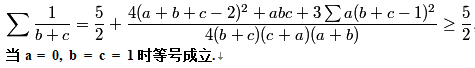（Chen  Ji )

事实上还可证明最大值:
$x,y,z\ge0,xy+yz+zx=1$时$\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\le\sqrt{\dfrac{27}{4}}$
提示:利用均值:$\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\le\sqrt{3\sum\dfrac{1}{(x+y)^2}}\le\sqrt{\dfrac{27}{4}}$
最后一步是著名的伊朗96不等式.
最后给一个利用上面方法的练习:(2011年全国联赛B卷二试第三题）

已知$a,b,c\ge1$且满足:$abc+2a^2+2b^2+2c^2+ca-cb-4a+4b-c=28,$求$a+b+c$的最大值.