Codeforces.297C.Splitting the Uniqueness(构造)

题目链接

\(Description\)

给定一个长为n的序列A，求两个长为n的序列B,C，对任意的i满足B[i]+C[i]=A[i]，且B,C序列分别至少有\(\lfloor\frac{2*n}{3}\rfloor\)个元素不同。

A中元素各不相同，Ai,Bi,Ci均为非负整数。

\(Solution\)

取\(k=\lfloor\frac{n}{3}\rfloor\)，将B,C序列分成三份。可以先将A进行排序。

B序列1_k取0k-1，C序列k+1_2k取k2k-1，C 2k+1_n取0k-1；B,C其余部分分别为Ai减去另一确定数组

这样可以满足C序列条件，对于2k+1_{n，Ai递增，Ci应是递减的，这样才能满足Bi是单调的(递增)，这样B不会在2k+1}n中出现重复。

最小值B[2k+1]=A[2k+1]-C[2k+1]>=k+1，即大于任意Bi(i∈[1,k])。

若Ai是各不相同的，那么一定有解；否则要讨论下。



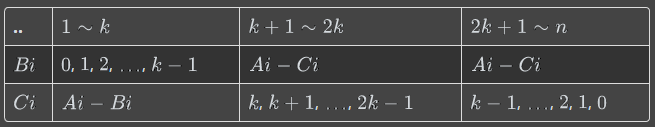
(博客园不会表格。。)

注意k不能单纯地取n/3，在有余数比如5的时候，序列1.2部分元素比3部分少，可能在3部分会有重复，在n比较大的时候这重复的两个元素就很致命了。

/*
		 1~k		   k+1~2k          2k+1~n
Bi	  0,1,2,...,k-1		Ai-Ci		     Ai-Ci
Ci		Ai-Bi		k,k+1,...,2k-1	k-1,...,2,1,0
*/
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define mp std::make_pair
const int N=1e5+5;

int n;
std::pair<int,int> A[N];
struct Answer
{
	int id,b,c;
	bool operator <(const Answer &x)const {return id<x.id;}
}ans[N];

inline int read()
{
	int now=0,f=1;register char c=gc();
	for(;!isdigit(c);c=gc()) if(c=='-') f=-1;
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now*f;
}

int main()
{
	n=read();
	for(int i=1; i<=n; ++i) A[i]=mp(read(),i);
	std::sort(A+1,A+1+n);
	int k=(n+2)/3;
	for(int i=1; i<=k; ++i) ans[i].b=i-1, ans[i].c=A[i].first-i+1, ans[i].id=A[i].second;
	for(int i=k+1; i<=k<<1; ++i) ans[i].c=i-1, ans[i].b=A[i].first-i+1, ans[i].id=A[i].second;
	for(int i=k<<1|1; i<=n; ++i) ans[i].c=n-i, ans[i].b=A[i].first-n+i, ans[i].id=A[i].second;
	std::sort(ans+1,ans+1+n);
	puts("YES");
	for(int i=1; i<n; ++i) printf("%d ",ans[i].b);
	printf("%d\n",ans[n].b);
	for(int i=1; i<n; ++i) printf("%d ",ans[i].c);
	printf("%d",ans[n].c);

	return 0;
}