QDUoj GZS的三角形 棋盘里的数学 思维+杨辉三角

1.

• 题目
• 我的提交

GZS的三角形

发布时间: 2015年9月6日 15:18   最后更新: 2016年6月26日 12:10   时间限制: 1000ms   内存限制: 256M

描述

机智无比的G神今天完成了一天的任务，实在是无聊的紧，拿起一支笔在纸上画起了三角形，边长为1， 2， 3，.........

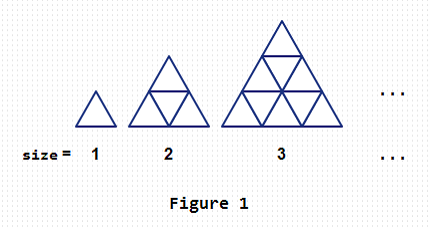
即使是无聊到这种程度，G神发达的大脑也在不停的思考，从顶部的点到沿着所画出的边到达底边的方案有多少种呢。

结果可能比较大， 结果对1000003取余。

例如，边长为2的情况如下所示：

输入

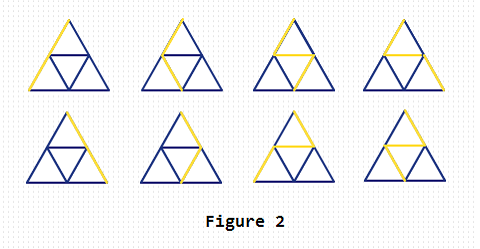
第一行有一个整数 T (1 <= T <= 1000) ，是三角形的个数。
接下来T行，每行一个整数 N (1 <= N <= 10^18)，代表三角形边长。

输出

输出T行，每行代表方案数，结果对1000003取余。

样例输入1 复制

3
1
2
3

样例输出1

2
8
48

规律如上：可以得到第n行即边长为n的ans[n] = 2 * ans[n-1] + (n-1) * 2*ans[n-1] = 2 * n * ans[n-1]。

但是直接这么做时间会爆，当 n >= 1000003时，对 1000003取余之后都为0。

1. #include <iostream>
2. #include <cstdio>
3. #define M 1000003
4. #define LL long long
5. using namespace std;
6. LL ans[M+5];
7. int main(){
8. int t, i;
9. LL n;
10. ans[1] = 2;
11. for(i = 2; i < M; ++i)
12. ans[i] = 2*i*ans[i-1] % M;
13. cin >> t;
14. while(t--){
15. scanf("%lld", &n);
16. if(n >= M){
17. printf("0\n");
18. continue;
19. }
20. printf("%lld\n", ans[n]);
21. }
22. return 0;
23. }

2.

• 题目
• 我的提交

棋盘里的数学

发布时间: 2016年9月13日 20:39   最后更新: 2016年9月20日 12:04   时间限制: 1000ms   内存限制: 128M

描述

lhcoder有一个n行m列的棋盘，有一颗棋子从左上角(1,1)开始移动，每次只能往右或者往下移动一格，到右下角(n,m)一共有多少移动方案?

输入

有多组测试数据，每组测试数据中有两个整数n和m(2 <= n, m <= 1000),代表为n行m列的棋盘。

输出

一个整数p，代表从左上角(1,1)移动到右下角(n,m)的方案数,由于方案数可能比较大，结果请对99991取模。

样例输入1 复制

2 2

样例输出1

2

样例输入2 复制

2 3

样例输出2

3

规律如下：当x = 1或y = 1时，该ans = 1；除此之外，(x, y)的ans = (x-1, y)的ans + (x, y-1)的ans。

1. #include <iostream>
2. #include <cstdio>
3. #define M 99991
4. #define LL long long
5. using namespace std;
6. LL a[1005][1005];
7. LL doo(int x, int y){
8. if(a[x][y] != 0) return a[x][y];
9. if(x == 1 || y == 1) return a[x][y] = 1;
10. else return a[x][y] = (doo(x-1, y) + doo(x, y-1)) % M;
11. }
12. int main(){
13. int n, m;
14. a[1][2] = a[2][1] = 1;
15. while(~scanf("%d %d", &n, &m)){
16. printf("%lld\n", doo(n, m));
17. }
18. return 0;
19. }