约数之和（POJ1845 Sumdiv）

最近应老延的要求再刷《算法进阶指南》（不得不说这本书不错）...这道题花费了较长时间~（当然也因为我太弱了）所以就写个比较易懂的题解啦~

原题链接：POJ1845

翻译版题目（其实是AcWing上的）：

假设现在有两个自然数A和B，S是A^B的所有约数之和。

请你求出S mod 9901的值是多少。

输入格式

在一行中输入用空格隔开的两个整数A和B。

输出格式

输出一个整数，代表S mod 9901的值。

数据范围

0≤A,B≤5×10⁷

输入样例：

2 3

输出样例：

15

注意: A和B不会同时为0。

首先看到这题就知道不能打暴力（这还用你说），那就需要找一个巧方法

那么，什么是约数呢？

约数嘛，顾名思义，可以约掉的数，其实就是因数

如果你连因数都不知道就只好自行百度了

但其实百度还挺有用的

以下是约数的定义：

约数，又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。在大学之前，"约数"一词所指的一般只限于正约数。约数和倍数都是二元关系的概念，不能孤立地说某个整数是约数或倍数。一个整数的约数是有限的。同时，它可以在特定情况下成为公约数。

但你再往下翻你会找到这个东西：

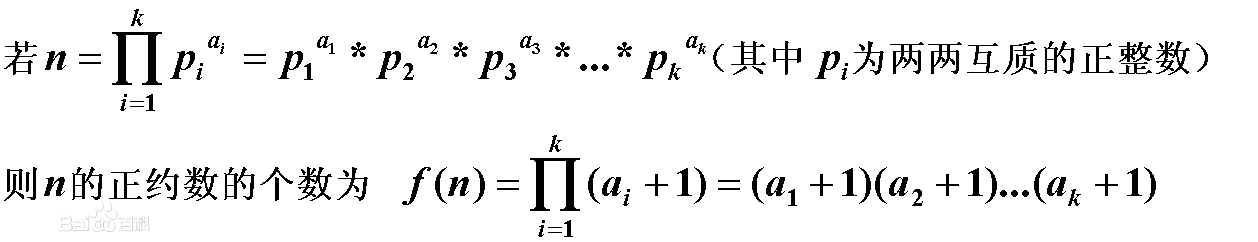
恩？这不就是质因数分解吗？

根据这个思路，我们很容易得到以下结论:

若A=P₁^c₁*P₂^c₂*...*P_n^c_n ,那么A^B就等于

P₁^B*c₁*P₂^B*c₂*...*P_n^B*c_n 

又因为A^B的约数集合可以看做其每一个质因数分别相乘得出的结果的集合

举个例子便于理解：

12=2²*3¹

所以12的因数集合为

{1，2，3，2*2，2*3，2*2*3}={1，2，3，4，6，12}

可以看做把12的质因数分别组合相乘

那么我们把这个式子加起来可以得到

1+2+3+2*2+2*3+2*2*3

稍微改造一下

（1+2+2*2）（1+3）

似乎有点眉目了？

那么A^B的约数之和由此可得：

（1+P₁+P₁²+....+P₁^B*c₁）*(1+P₂+P₂²+....+P₂^B*c₂)*....*(1+P_n+P_n²+....+P_n^B*c_n)

(这段真他喵的难打)

根据同余定理，我们在求A^B%9901就相当于以上每一个式子%9901再相乘

那么问题就又到了如何求（1+P+P²+....+P^c）

因为同余对于除法没有分配率，所以这道题不能使用等比数列求和公式....

所以这时候我们想到了.....

分治！

将求解（1+P+P²+....+P^c）定义为sum（p,c），则有：

当c为奇数时：

sum（p，c）=（1+P+....+P^（c-1）/2）+（1+P^（c+1）/2+...+P^c）

                     =（1+P+....+P^（c-1）/2）+P^（c+1）/2 _*（1+P+....+P^（c-1）/2）

                     =（1+P^（c+1）/2）*（1+P+....+P^（c-1）/2）

当c为偶数时，同理得：

sum（p，c）=（1+P^c/2）*（1+P+....+P^c/2-1）+P^c

（打这个更累！！！！）

这样，我们在每次求解时都可以将问题简化，配合快速幂就可以用θ（log n）的时间复杂度得到正确答案

.....

所以，你应该会分解质因数吧？

......

不会吗？

orz

---

由此可见，虽然我们知道了具体解法，但码出代码好像还有点问题....

但其实分解质因数是相当简单的！（而且时间复杂度只有θ（n）（大概吧））

相信大家都会判断一个数是否是质数~

那就是从2试到根号n，若有n可以整除的则n不是质数，若没有则n为质数

同理，我们可以从2开始试n的因子（试到根号n），然后除掉所有的因子并计数

（这种算法叫试除法）

以下代码：

    int m=;
    for(int i=;i<=sqrt(n);i++)
    {
        if(n%i==)
        m++,yz[m]=i;//yz数组存分解出的因子
        while(n%i==)//除掉所有的i
        {
            n/=i;
            gs[m]++;//gs数组存每个因子的个数
        }
    }
    if(n>)
    m++,yz[m]=n,gs[m]=;
    for(int i=;i<=m;i++)
    printf("%d^%d\n",yz[i],gs[i]);

还有一种更优的算法，叫做“Pollard's Rho”算法，但有点复杂（我懒得写），可以自行去查 已经帮你查好了←

那么这道题就可以写出来了~（我相信你会快速幂）

以下AC代码

#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
using namespace std;
const int N=;
int  yz[],gs[];//分别用来存储质因子及其个数
int quick(int a,int b)//快速幂
{
    long long t;
    if(b==)return a%N;
    if(b%==)
    {
        t=quick(a,b/);
        return t%N*t%N;
    }
    else
    {
        t=quick(a,b/);
        t=t%N*t%N;
        t=t%N*a%N;
        return t%N;
    }
}
long long sum(int p,int c)
{
    if(c==) return ;//边界
    if(c==) return p+;//边界*2,可写可不写，开始没加1出了点问题
    if(c%)
    return (+quick(p,(c+)/))%N*sum(p,c/)%N;//奇数
    else
    return (+quick(p,c/))%N*sum(p,c/-)%N+quick(p,c);//偶数
}
long long czs(int n,int b)//分解质因数
{
    if(n==) return ;//特殊情况直接返回
    if(b==) return ;
    int m=,ans=;
    for(int i=;i<=sqrt(n);i++)
    {
        if(n%i==)
        m++,yz[m]=i;
        while(n%i==)
        {
            n/=i;
            gs[m]++;
        }
    }
    if(n>)
    m++,yz[m]=n,gs[m]=;
    for(int i=;i<=m;i++)
    ans=(ans%N*sum(yz[i],gs[i]*b)%N)%N;
    return ans%N;
}
int main()
{
    int a,b;
    scanf("%d%d",&a,&b);
    printf("%lld",czs(a,b)%N);
    return ;
}
//写这么多%N是因为数据溢出www
//那个数据在下方，可以试一试能不能过
//输入：50000000 50000000
//输出：5531

终于完了 赶紧刷B站学习去了

感谢观看~ヽ(￣▽￣)ﾉ