实验6 Bezier曲线生成

1．实验目的：

了解曲线的生成原理，掌握几种常见的曲线生成算法，利用VC+OpenGL实现Bezier曲线生成算法。

2．实验内容：

（1） 结合示范代码了解曲线生成原理与算法实现，尤其是Bezier曲线；

（2） 调试、编译、修改示范程序。

3．实验原理：

Bezier曲线是通过一组多边形折线的顶点来定义的。如果折线的顶点固定不变，则由其定义的Bezier曲线是唯一的。在折线的各顶点中，只有第一点和最后一点在曲线上且作为曲线的起始处和终止处，其他的点用于控制曲线的形状及阶次。曲线的形状趋向于多边形折线的形状，要修改曲线，只要修改折线的各顶点就可以了。因此，多边形折线又称Bezier曲线的控制多边形，其顶点称为控制点。

三次Bezier曲线，有四个控制点，其数学表示如下：

，

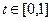
4．实验代码：

 #include <GL/glut.h>

 #include <stdio.h>

 #include <stdlib.h>

 #include <vector>

 using namespace std;

 struct Point {

 int x, y;

 };

 Point pt[], bz[];

 vector<Point> vpt;

 bool bDraw;

 int nInput;

 void CalcBZPoints()

 {

 float a0,a1,a2,a3,b0,b1,b2,b3;

 a0=pt[].x;

 a1=-*pt[].x+*pt[].x;

 a2=*pt[].x-*pt[].x+*pt[].x;

 a3=-pt[].x+*pt[].x-*pt[].x+pt[].x;

 b0=pt[].y;

 b1=-*pt[].y+*pt[].y;

 b2=*pt[].y-*pt[].y+*pt[].y;

 b3=-pt[].y+*pt[].y-*pt[].y+pt[].y;

 float t = ;

 float dt = 0.01;

 for(int i = ; t<1.1; t+=0.1, i++)

 {

 bz[i].x = a0+a1*t+a2*t*t+a3*t*t*t;

 bz[i].y = b0+b1*t+b2*t*t+b3*t*t*t;

 }

 }

 void ControlPoint(vector<Point> vpt)

 {

 glPointSize();

 for(int i=; i<vpt.size(); i++)

 {

 glBegin (GL_POINTS);

 glColor3f (1.0f, 0.0f, 0.0f); glVertex2i (vpt[i].x,vpt[i].y);

 glEnd ();

 }

 }

 void PolylineGL(Point *pt, int num)

 {

 glBegin (GL_LINE_STRIP);

 for(int i=;i<num;i++)

 {

 glColor3f (1.0f, 1.0f, 1.0f);

 glVertex2i (pt[i].x,pt[i].y);

 }

 glEnd ();

 }

 void myDisplay()

 {

 glClear(GL_COLOR_BUFFER_BIT);

 glColor3f (1.0f, 1.0f, 1.0f);

 if (vpt.size() > ) {

 ControlPoint(vpt);

 }

 if(bDraw)

 {

 PolylineGL(pt, );

 CalcBZPoints();

 PolylineGL(bz, );

 }

 glFlush();

 }

 void Init()

 {

 glClearColor(0.0, 0.0, 0.0, 0.0);

 glShadeModel(GL_SMOOTH);

 printf("Please Click left button of mouse to input control point of Bezier Curve!\n");

 }

 void Reshape(int w, int h)

 {

 glViewport(, , (GLsizei) w, (GLsizei) h);

 glMatrixMode(GL_PROJECTION);

 glLoadIdentity();

 gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);

 }

 void mouse(int button, int state, int x, int y)

 {

 switch (button)

 {

 case GLUT_LEFT_BUTTON:

 if (state == GLUT_DOWN)

 {

 if (nInput == )

 {

 pt[].x = x;

 pt[].y =  - y;

 nInput = ;

 vpt.clear();

 vpt.push_back(pt[]);

 bDraw = false;

 glutPostRedisplay();//

 }

 else if (nInput == )

 {

 pt[].x = x;

 pt[].y =  - y;

 vpt.push_back(pt[]);

 nInput = ;

 glutPostRedisplay();//

 }

 else if (nInput == )

 {

 pt[].x = x;

 pt[].y =  - y;

 vpt.push_back(pt[]);

 nInput = ;

 glutPostRedisplay();//

 }

 else if (nInput == )

 {

 pt[].x = x;

 pt[].y =  - y;

 bDraw = true;

 vpt.push_back(pt[]);

 nInput = ;

 glutPostRedisplay();//

 }

 }

 break;

 default:

 break;

 }

 }

 int main(int argc, char *argv[])

 {

 glutInit(&argc, argv);

 glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);

 glutInitWindowPosition(, );

 glutInitWindowSize(, );

 glutCreateWindow("Hello World!");

 Init();

 glutDisplayFunc(myDisplay);

 glutReshapeFunc(Reshape);

 glutMouseFunc(mouse);

 glutMainLoop();

 return ;

 }

附上本实验的VC++工程代码（VC++2008）

5．实验提高

尝试实现B样条曲线算法。